Can a concave polygon be Equiangular? A polygon that is regular is both equilateral AND equiangular. A regular triangle
Triangle
A triangle is a polygon with three edges and three vertices. It is one of the basic shapes in geometry. A triangle with vertices A, B, and C is denoted △ABC. In Euclidean geometry any three points, when non-collinear, determine a unique triangle and simultaneously, a unique plane. In other wor…
Full Answer
Are regular polygons ever concave?
Hence, regular polygons are never concave. Let us discuss the formulas such as area and the perimeter of the concave polygon below. Unlike a regular polygon, there is no easy formula to find the area of a concave polygon.
Do equiangular polygons have the same angles?
Equilateral polygons with more that four sides are also usually equiangular. If the sides are all the same length, then they also have the same angle measurement. This is not true, however, if one or more of their angles are 'pushed in', like the red angle shown in the pentagon picture.
What are the interior angles of a concave polygon?
A concave polygon has one or more of its vertices “pushed inside”. Hence, they point towards the interior of the polygon The interior angles of any polygon always add up to a constant value, which depends only on the number of sides of the polygon.
What is the perimeter of a concave polygon?
Similarly, the perimeter of a concave polygon is defined as the total distance covered around the boundary of the concave polygon. The perimeter of a concave polygon can be found by adding together the length of all the sides.
Can concave polygons be equilateral?
However, equilateral pentagons, and equilateral polygons with more than five sides, can also be concave, and if concave pentagons are allowed then two angles are no longer sufficient to determine the shape of the pentagon.
Can a convex polygon be equiangular?
A rectangle, <4>, is a convex direct equiangular polygon, containing four 90° internal angles. A concave indirect equiangular polygon, <6-2>, like this hexagon, counterclockwise, has five left turns and one right turn, like this tetromino.
Can a polygon be equiangular but not?
Mathematical background However, this is not the case for all polygons. For example, a rectangle is equiangular — all four angles are 90° — but need not be square (need not have all four sides the same length). Thus, not all equiangular quadrilaterals are equilateral and so are not all regular.
Can a polygon be equiangular?
In Euclidean geometry, an equiangular polygon is a polygon whose vertex angles are equal. If the lengths of the sides are also equal (that is, if it is also equilateral) then it is a regular polygon. Isogonal polygons are equiangular polygons which alternate two edge lengths.
Can a polygon be concave?
A concave polygon is a polygon that is not convex. . An example of a non-simple (self-intersecting) polygon is a star polygon. A concave polygon must have at least four sides.
Are concave polygons irregular?
A Concave polygon is a polygon that has at least one interior angle greater than 180 degrees. It must have at least four sides. The shape of the concave polygon is usually irregular.
What shape is always equiangular?
For example, equilateral triangles have all congruent sides - that's the definition of equilateral . All their angles are the same also, which makes them equiangular . For triangles, it turns out that being equilateral and equiangular always go together.
Which polygons can be equiangular but not equilateral?
On the other hand, it is easy to conceive of an equiangular quadrilateral that is not equilateral, i.e. a rectangle.
What is concave and convex polygon?
The difference between convex and concave polygons lies in the measures of their angles. For a polygon to be convex, all of its interior angles must be less than 180 degrees. Otherwise, the polygon is concave.
What polygons are equiangular?
In Euclidean geometry, an equiangular polygon is a polygon whose vertex angles are equal. If the lengths of the sides are also equal then it is a regular polygon. The only equiangular triangle is the equilateral triangle. Rectangles, including the square, are the only equiangular quadrilaterals (four-sided figures).
Are all regular polygons equiangular?
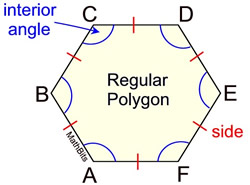
Regular polygons are both equiangular and equilateral, so all angles in it are congruent and all sides are congruent.
Are all equilateral are equiangular?
Every equilateral triangle is also an isosceles triangle, so any two sides that are equal have equal opposite angles. Therefore, since all three sides of an equilateral triangle are equal, all three angles are equal, too. Hence, every equilateral triangle is also equiangular.
What shapes are equiangular?
Equiangular and Equilateral Rectangles are equiangular because all four angles are 90°. The sides don't have to be equal lengths for the polygon to be equiangular. Some polygons like to have all their sides the same length, they are called equilateral.
Which polygon is equilateral and equiangular?
A squareWhen a polygon is both equilateral and equiangular, it is called a regular polygon. A square is an example of a regular polygon.
What kind of polygon is always convex?
Note that a triangle (3-gon) is always convex. A convex polygon is the opposite of a concave polygon.
Can an equilateral triangle be equiangular?
Every equilateral triangle is also an isosceles triangle, so any two sides that are equal have equal opposite angles. Therefore, since all three sides of an equilateral triangle are equal, all three angles are equal, too. Hence, every equilateral triangle is also equiangular.
What shapes are equiangular and equilateral?
Shapes that are both equiangular as well as equilateral are known as regular polygons. Such shapes have a minimum of three sides.
How do you know if a polygon is equilateral?
A polygon is equilateral if all sides are the same length. Equilateral polygons are not necessarily equiangular but may be equiangular as well.
What is the difference between a regular polygon and an equilateral polygon?
A regular polygon must be equilateral as well as equiangular, but an equilateral polygon is not necessarily equiangular, that is, regular polygons...
Is every equiangular polygon convex?
Every equiangular polygon is convex. In order to have a convex polygon, it is necessary for all interior angles to measure less than 180 degrees. A...
What is the meaning of equiangular polygon in geometry?
The term equiangular comes from the Latin words equi- , meaning same, and angulus , meaning having a corner. Thus, an equiangular polygon in wh...
What is the equiangular polygon formula?
The sum of the angles in an equiangular polygon may be found with the formula S=(n-2) x 180 degrees, where n is the number of sides in a polygon.
How many left turns does an equiangular hexagon have?
An indirect equiangular hexagon, <6-6> 90° with 3 left turns, 3 right turns, totaling 0°. In Euclidean geometry, an equiangular polygon is a polygon whose vertex angles are equal. If the lengths of the sides are also equal (that is, if it is also equilateral) then it is a regular polygon.
What is an equiangular polygon?
An equiangular polygon can be constructed from a regular polygon or regular star polygon where edges are extended as infinite lines. Each edges can be independently moved perpendicular to the line's direction. Vertices represent the intersection point between pairs of neighboring line.
What is an isogonal polygon?
Isogonal polygons are equiangular polygons which alternate two edge lengths. For clarity, a planar equiangular polygon can be called direct or indirect. A direct equiangular polygon has all angles turning in the same direction in a plane and can include multiple turns. Convex equiangular polygons are always direct.
How many turns does a skew polygon have?
A multi-turning equiangular polygon can be direct, like this octagon, <8/2>, has 8 90° turns, totaling 720°. A concave indirect equiangular polygon, <5-2>, counterclockwise has 4 left turns and one right turn.
How many angles does a rectangle have?
A rectangle, <4>, is a convex direct equiangular polygon, containing four 90° internal angles. A concave indirect equiangular polygon, <6-2>, like this hexagon, counterclockwise, has five left turns and one right turn, like this tetromino . A skew polygon has equal angles off a plane, like this skew octagon alternating red and blue edges on a cube .
What does a vertice represent?
Vertices represent the intersection point between pairs of neighboring line. Each moved line adjusts its edge-length and the lengths of its two neighboring edges. If edges are reduced to zero length, the polygon becomes degenerate, or if reduced to negative lengths, this will reverse the internal and external angles.
Is a cyclic polygon equiangular?
A cyclic polygon is equiangular if and only if the alternate sides are equal (that is, sides 1, 3, 5, ... are equal and sides 2, 4, ... are equal). Thus if n is odd, a cyclic polygon is equiangular if and only if it is regular. For prime p, every integer-sided equiangular p -gon is regular.
Equilateral Polygon Definition
Equilateral polygon definition: An equilateral polygon is one having sides of equal length. An equilateral triangle, for example, has three sides of the same length, while a square has four. The term equilateral is derived from the Latin words equi -, or same, and latus, or side.
Equiangular Polygon Definition
Equiangular polygon definition: An equiangular polygon is one having the same, or congruent, interior angles, although it may also be said that, by reciprocity, the exterior angles may also all be the same. An equiangular triangle may have three 60-degree inner angles, but it is also true that it has six 120-degree exterior angles.
Equiangular Triangle Definition
Equiangular Triangle Definition: An equiangular triangle is one in which the three interior angles all measure 60 degrees. The three interior angles must add up to 180 degrees.
What is the difference between a convex and a concave polygon?
For a polygon to be convex, all of its interior angles must be less than 180 degrees. Otherwise, the polygon is concave.
What is the center of a regular polygon?
The center of a regular polygon is the point from which all the vertices of the polygon are equidistant. Regular polygons have special properties that we'll explore in the next section. Below are some examples of equiangular, equilateral, and regular polygons. Figure %: Equilateral, equiangular, and regular polygons.
Where are the diagonals of a convex polygon?
Another way to think of it is this: the diagonals of a convex polygon will all be in the interior of the polygon, whereas certain diagonals of a concave polygon will lie outside the polygon, on its exterior. Below in Part A are some convex polygons, and in Part B, some concave polygons.
Is a polygon a square?
Equiangular polygons have congruent interior angles, like a rectangle. When a polygon is both equilateral and equiangular, it is called a regular polygon. A square is an example of a regular polygon.
Why are all equilateral triangles equiangular?
Because of how rigid and structured a triangle is , all equilateral triangles are also equiangular. Every equilateral triangle has three 60-degree angles inside the triangle and three 120-degree angles outside the triangle. Equilateral and Equiangular Four-Sided Polygons (quadrilaterals)
What is an equiangular polygon?
An equiangular polygon (from Latin aequi meaning ''equal'' and angularis meaning ''having corners or sides'' ) is a figure with straight sides, like other polygons, but in this figure every internal angle has the same measure. For example, rooms in a typical house usually have square corners; that is, the measure of every corner is 90 degrees.
What does an ice cube look like?
Imagine an ice cube—a perfectly square frozen block of ice, sitting on the desk. If you look at it, straight on from the top, you'll see that it looks like a square. Its sides all measure the same length. Its edges all come together to make perfectly square corners, 90 degrees, just like the corners of a typical house. The top of that ice cube—if it's a perfectly square one—forms one kind of equilateral and equiangular polygon.
What is a quadrilateral with 4 sides called?
Equilateral quadrilaterals (or four-sided polygons) all have four equal sides, regardless of the angles between the sides. Also called a rhombus, these figures are either a square, in which case all four angles also are equal, or a non-square rhombus. Other Equiangular and Equilateral Polygons.
What does it mean when a polygon is concave?
If it's concave, that means that at least one angle is more than 180 degrees (meaning more than a straight line) and looks bent backward like the one in the pentagon with the red angle. ...
How many sides does a polygon have?
As we learned, polygons are geometric figures with straight sides. They will have at least three sides, and may have many more. Remember: ''equi'' means equal, ''lateral'' means sides, and ''angular'' means angles. Therefore, if all of the sides of the polygon are the same length, the polygon is said to be equilateral, ...
Which polygon has more than 4 sides?
Other Equiangular and Equilateral Polygons. Equilateral polygons with more than four sides are also usually equiangular. If the sides are all the same length, then they also have the same angle measurement.
What are the endpoints of a polygon called?
The endpoints of the sides of polygons are called vertices. When naming a polygon, its vertices are named in consecutive order either clockwise or counterclockwise. Consecutive sides are two sides that have an endpoint in common. The four‐sided polygon in Figure could have been named ABCD, BCDA, or ADCB, for example.
How many sides does a triangle have?
The following lists the different types of polygons and the number of sides that they have: A triangle is a three‐sided polygon. A quadrilateral is a four‐sided polygon. A pentagon is a five‐sided polygon.
When a polygon is both equilateral and equiangular, it is referred to as
When a polygon is both equilateral and equiangular, it is referred to as a regular polygon. For a polygon to be regular, it must also be convex. Figure shows examples of regular polygons.
What is a closed shape called?
Classifying Polygons. Closed shapes or figures in a plane with three or more sides are called polygons. Alternatively, a polygon can be defined as a closed planar figure that is the union of a finite number of line segments. In this definition, you consider closed as an undefined term.
Is an octagon a nonagon?
An octagon is an eight‐sided polygon. A nonagon is a nine‐sided polygon. A decagon is a ten‐sided polygon. An earlier chapter showed that an equilateral triangle is automatically equiangular and that an equiangular triangle is automatically equilateral. This does not hold true for polygons in general, however.
Is a polygon closed or undefined?
In this definition, you consider closed as an undefined term. The term polygon is derived from a Greek word meaning “many‐angled.”. Polygons first fit into two general categories— convex and not convex (sometimes called concave ).
Overview
Equiangular polygon theorem
For a convex equiangular p-gon, each internal angle is 180(1-2/p)°; this is the equiangular polygon theorem.
For a direct equiangular p/q star polygon, density q, each internal angle is 180(1-2q/p)°, with 1<2q<p. For w=gcd(p,q)>1, this represents a w-wound (p/w)/(q/w) star polygon, which is degenerate for the regular case.
Construction
An equiangular polygon can be constructed from a regular polygon or regular star polygon where edges are extended as infinite lines. Each edges can be independently moved perpendicular to the line's direction. Vertices represent the intersection point between pairs of neighboring line. Each moved line adjusts its edge-length and the lengths of its two neighboring edges. If edges are reduced to zero length, the polygon becomes degenerate, or if reduced to negative lengths, this …
Notation
Every direct equiangular p-gon can be given a notation <p> or <p/q>, like regular polygons {p} and regular star polygons {p/q}, containing p vertices, and stars having density q.
Convex equiangular p-gons <p> have internal angles 180(1-2/p)°, while direct star equiangular polygons, <p/q>, have internal angles 180(1-2q/p)°.
A concave indirect equiangular p-gon can be given the notation <p-2c>, with c counter-turn vertic…
Other properties
Viviani's theorem holds for equiangular polygons:
The sum of distances from an interior point to the sides of an equiangular polygon does not depend on the location of the point, and is that polygon's invariant.
A cyclic polygon is equiangular if and only if the alternate sides are equal (that is, sides 1, 3, 5, ... are equal and sides 2, 4, ... are equal). Thus if n is odd, a cyclic polygon is equiangular if and onl…
Direct equiangular polygons by sides
Direct equiangular polygons can be regular, isogonal, or lower symmetries. Examples for <p/q> are grouped into sections by p and subgrouped by density q.
Equiangular triangles must be convex and have 60° internal angles. It is an equilateral triangle and a regular triangle, <3>={3}. The only degree of freedom is edge-length.
See also
• Spirolateral
External links
• A Property of Equiangular Polygons: What Is It About? a discussion of Viviani's theorem at Cut-the-knot.
• Weisstein, Eric W. "Equiangular Polygon". MathWorld.