a) since the standard normal curve is symmetric and centred around μ , 50% of the curve lies at the left of μ and 50% lies to the right b) according to the 68-95-99 rule, 68% of the standard normal curve lies from μ − σ and μ + σ
Full Answer
What percentage of the measures are below the normal curve?
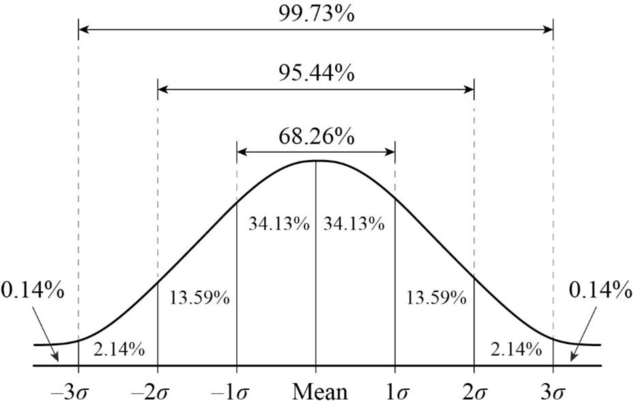
95% of the measures are within 2 standard deviation of the mean. 99.7% of the measures are within 3 standard deviations of the mean. The normal distribution is also symmetric, which means that 50% of the measures are below the mean and 50% are above. a) What percentage of the area under the normal curve lies to the left of μ?
What is the area under the standard normal curve to Z?
The area under the standard normal curve to the left of z = 1.26 is 0.8962. Question: Find the area under the standard normal curve to the right of z = -1.81.
What percentage of measures are within 3 standard deviations of the mean?
99.7% of the measures are within 3 standard deviations of the mean. The normal distribution is also symmetric, which means that 50% of the measures are below the mean and 50% are above. a) What percentage of the area under the normal curve lies to the left of μ?
How do you find the area less than some value?
Example 1: Find the Indicated Area Less Than Some Value. Question: Find the area under the standard normal curve to the left of z = 1.26. Solution: To answer this question, we simply need to look up the value in the z table that corresponds to 1.26: The area under the standard normal curve to the left of z = 1.26 is 0.8962.
What is the percentage of the area under the normal curve lies?
68%In general, about 68% of the area under a normal distribution curve lies within one standard deviation of the mean. That is, if ˉx is the mean and σ is the standard deviation of the distribution, then 68% of the values fall in the range between (ˉx−σ) and (ˉx+σ) .
What percentage of the area under the normal curve lies to the left μ 3σ and right of μ+ 3σ?
Note that 218 = μ - 3σ. The area between (μ - 3σ) and (μ + 3σ) is approximately 99.7%; thus, the area outside of that (less than μ - 3σ or greater than μ + 3σ) must be about 0.3%.
What percent of the area under the normal curve lies within 0.5 standard deviations from the mean?
Reading from the chart, it can be seen that approximately 19.1% of normally distributed data is located between the mean (the peak) and 0.5 standard deviations to the right (or left) of the mean. This chart shows only percentages that correspond to subdivisions up to one-half of one standard deviation.
How do you find the area under the standard normal curve that lies?
0:133:46Finding the Area Under a Standard Normal Curve Using the TI-84YouTubeStart of suggested clipEnd of suggested clipAnd then bars. And then normal CDF is number two so we press ENTER. And with this you want to putMoreAnd then bars. And then normal CDF is number two so we press ENTER. And with this you want to put the lower bound first and then the upper bound well we can't put negative infinity as a lower bound.
What percentage of the area under a normal curve is within 2 standard deviations of the mean?
Regardless of what a normal distribution looks like or how big or small the standard deviation is, approximately 68 percent of the observations (or 68 percent of the area under the curve) will always fall within two standard deviations (one above and one below) of the mean.
What portion of the area under the normal curve lies within one standard deviation from the mean?
68%For the standard normal distribution, 68% of the observations lie within 1 standard deviation of the mean; 95% lie within two standard deviation of the mean; and 99.9% lie within 3 standard deviations of the mean.
What percent of the area under a normal curve is within 3 standard deviations?
99.7%Approximately 99.7% of the data fall within three standard deviations of the mean.
What value is 0.5 standard deviations above the mean?
Explanation: For a normal distribution, if we are using the standard normal distribution N(0,12) , a z-score of +0.5 represents a half of a standard deviation above the mean μ .
What percent of the area under a normal curve is within 3 standard?
99.7%The Empirical Rule states that 99.7% of data observed following a normal distribution lies within 3 standard deviations of the mean. Under this rule, 68% of the data falls within one standard deviation, 95% percent within two standard deviations, and 99.7% within three standard deviations from the mean.
How do you find the percentage of a normal distribution?
0:329:49Using Table A to find Percent of Data in a Normal Distribution - YouTubeYouTubeStart of suggested clipEnd of suggested clipOkay the formula is right here. So let's calculate it it's going to my value my z-score sorry my ZMoreOkay the formula is right here. So let's calculate it it's going to my value my z-score sorry my Z is equal to 50 is my value minus the mean divided by the standard deviation.
How do you find the z-score of a percentage?
To find the Z-score, you subtract class mean (50 percent) from the individual score (80 percent) and divide the result by the standard deviation.
Answer
a) since the standard normal curve is symmetric and centred around μ , 50% of the curve lies at the left of μ and 50% lies to the right
Answer
The Empirical Rule states that, for a normally distributed random variable:
New questions in Mathematics
The radius of a circle is 1 meter. What is the area? r=1 m Give the exact answer in simplest form.
Example 1: Find the Indicated Area Less Than Some Value
Question: Find the area under the standard normal curve to the left of z = 1.26.
Example 2: Find the Indicated Area Greater Than Some Value
Question: Find the area under the standard normal curve to the right of z = -1.81.
Example 3: Find the Indicated Area Between Two Values
Question: Find the area under the standard normal curve between z = -1.81 and z = 1.26
Example 4: Find the Indicated Area Outside of Two Values
Question: Find the area under the standard normal curve outside of z = -1.81 and z = 1.26
Bonus: The Standard Normal Curve Area Calculator
You can use this calculator to automatically find the area under the standard normal curve between two values.