How to find out the end behavior of a function?
There are three main types of end behavior:
- Infinite: limit of the function goes to infinity (either positive or negative) as x goes to infinity. ...
- Finite: The limit of the function goes to some finite number as x goes to infinity. ...
- There are also cases where the limit of the function as x goes to infinity does not exist; these are typically oscillating functions like the sine function. ...
What is the formula for end behavior?
term, the end behavior is the same as the function f(x) = −3x. For large positive values of x, f(x) is large and negative, so the graph will point down on the right. Similarly, the graph will point up on the left, as o n the left of Figure 1. On the other hand, if we have the function f(x) = x2 +5x+3, this has the same end behavior as f(x) = x2,
What does a function's end behavior mean?
What's "end behavior"? The end behavior of a function describes the behavior of the graph of the function at the "ends" of the -axis . In other words, the end behavior of a function describes the trend of the graph if we look to the right end of the -axis (as approaches ) and to the left end of the -axis (as approaches ).
How would you describe the end behavior?
Determining end behavior algebraically
- Investigation: End behavior of monomials. Monomial functions are polynomials of the form , where is a real number and is a nonnegative integer.
- Concluding the investigation. Notice how the degree of the monomial and the leading coefficient affect the end behavior. ...
- End behavior of polynomials. We now know how to find the end behavior of monomials. ...
How to find the end behavior of a rational function?
Determining the End Behavior of a Rational Function. Step 1: Look at the degrees of the numerator and denominator. If the degree of the denominator is larger than the degree of the numerator, there is a horizontal asymptote of {eq}y = 0 {/eq}, which is the end behavior of the function. Step 2: If the degrees of the numerator ...
What is the horizontal asymptote of a function?
If the degree of the denominator is larger than the degree of the numerator, there is a horizontal asymptote of {eq}y = 0 {/eq}, which is the end behavior of the function. The degree of the numerator is 4, and the degree of the denominator is 3. Move to the next step.
What is the asymptote of a function when the degree of the numerator is greater than
The degrees are not equal - move to the next step. Step 3: If the degree of the numerator is greater than the degree of the denominator, then there is a slant/oblique asymptote (if the degree of the numerator is exactly one larger than the degree of the denominator), or the function is asymptotic to a polynomial.
End behavior of rational functions Definition
A polynomial function f (x) is a polynomial in x. A rational function can be written as the ratio of two polynomial functions P (x) and Q (x).
Overview of End Behavior Of Rational Functions
To analyze the end behavior of rational functions, we first need to understand asymptotes. A line is said to be an asymptote to a curve if the distance between the line and the curve slowly approaches zero as x increases. An asymptote helps to ‘model’ the behaviour of a curve.
Asymptotes in a graph
When the input value of x approaches zero from the left side, f (x) keeps decreasing and approaches negative infinity. When x approaches zero from the right side, f (x) approaches positive infinity.
Common notations
The asymptotic behavior of graphs is indicated using the symbols below.
Asymptotes of a rational function
The function has been plotted in red. The function becomes undefined at x=-1. The blue dotted line in the graph shows a vertical asymptote at x=-1.
Example of a rational function
The equations of the oblique asymptotes and the end behavior polynomials are found by dividing the polynomial P (x) by Q (x). The remainder is ignored, and the quotient is the equation for the end behavior model. Rational functions may or may not intersect the lines or polynomials which determine their end behavior.
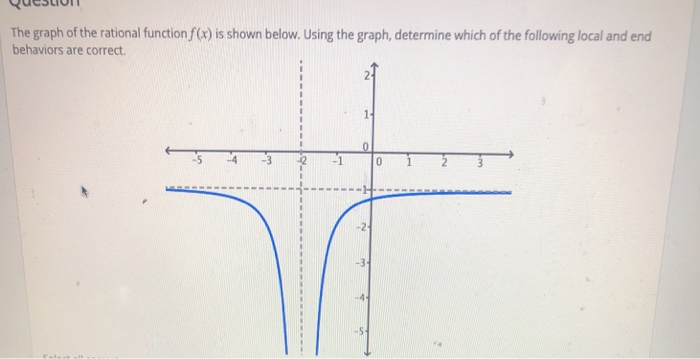
Determining The End Behavior of A Rational Function
Determining The End Behavior of A Rational Function - Vocabulary and Equations
- Rational Function:A rational function is a function made up of a ratio of polynomials. Rational functions are of the form {eq}f(x) = \dfrac{p(x)}{q(x)}{/eq}, where {eq}p(x){/eq} and {eq}q(x){/eq} are polynomials, and {eq}q(x) \neq 0{/eq}. End Behavior:The end behavior of a graph of a function is how the graph behaves as {eq}x{/eq} approaches infinity or negative infinity. The end behavio…
Example Problem 1: Determining The End Behavior of A Rational Function
- Determine the end behavior of the rational function. {eq}f(x) = \dfrac{4x^3 + 3x^2 - 2x - 1}{2x^3 + 3x - 4}{/eq} Step 1:Look at the degrees of the numerator and denominator. If the degree of the denominator is larger than the degree of the numerator, there is a horizontal asymptote of {eq}y = 0{/eq}, which is the end behavior of the function. The degree of the numerator is 3 and the degre…
Example Problem 2: Determining The End Behavior of A Rational Function
- Determine the end behavior of the rational function. {eq}f(x) = \dfrac{x^4 + 3x^2 - 1}{2x^3 + 5x}{/eq} Step 1:Look at the degrees of the numerator and denominator. If the degree of the denominator is larger than the degree of the numerator, there is a horizontal asymptote of {eq}y = 0{/eq}, which is the end behavior of the function. The degree of the numerator is 4, and the degre…