How to define ellipse?
What is an Ellipse?
- Definition of Ellipse. If we speak in terms of locus an ellipse can be defined as, it is the set of all points on the XY-plane, whose distance from any ...
- Equation of an Ellipse
- Things You Need to Know About an Ellipse. ...
- Area of Ellipse. ...
- Questions to Be Solved. ...
What is an example of an ellipse?
What is an Ellipse?
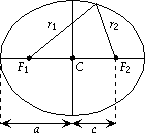
- An ellipse can be defined as the locus of all those points in a plane such that the sum of their distances from any two given fixed points in the ...
- The foci (singular focus) are the fixed points, which are surrounded by the curve.
- The shape of the ellipse is in an oval shape and the major axis and minor axis define its area.
When to use ellipses with useful rules?
- I know I saw my keys somewhere . . .
- I never thought . . .
- "I'm not sure what to do . . .," he said.
What is the difference between an ellipse and a circle?
Main Differences Between Circle and Ellipse
- A circle has the same distance from any point on the circumference to the center. ...
- A circle has a fixed shape of a figure even if the viewpoint is moved. ...
- A circle has a fixed radius that does not change its position. ...
- The radius of a circle is at the center, but the two foci of an ellipse lie at either end of an ellipse.
What is the special case of an ellipse?
Ellipses are a class of mathematical shapes. The circle is the special case of the ellipse that happens when the two foci (and the center) are co-incident. The number that characterizes how flat the ellipse looks is called the eccentricity, denoted by the letter e .
What is the perihelion distance?
The perihelion distance is a (1-e) and the aphelion distance is a (1+e). For example, the Earth's eccentricity is 0.017 and its semimajor axis is 1.000 A.U., so its perihelion distance is (1-0.017)a, or 0.983 A.U. Similarly, Earth's aphelion distance is 1.017 A.U.
What is the first law of astronomy?
Introductory Astronomy: Ellipses. (And you'd better not confuse ellipses with eclipses!) Kepler's first law is that planets orbit on ellipses with the sun at one focus. An ellipse is (sort of) an oval shape, with two interior points called foci (singular: focus), a long axis (the major axis), a short axis (the minor axis), ...
What is the ellipse in geometry?
In analytic geometry, the ellipse is defined as a quadric: the set of points#N#( X , Y ) { displaystyle ( X,,Y)}#N# of the Cartesian plane that , in non-degenerate cases, satisfy the implicit equation
What is an elliptical gear?
Two non-circular gears with the same elliptical outline, each pivoting around one focus and positioned at the proper angle, turn smoothly while maintaining contact at all times. Alternatively, they can be connected by a link chain or timing belt, or in the case of a bicycle the main chainring may be elliptical, or an ovoid similar to an ellipse in form. Such elliptical gears may be used in mechanical equipment to produce variable angular speed or torque from a constant rotation of the driving axle, or in the case of a bicycle to allow a varying crank rotation speed with inversely varying mechanical advantage .
What happens when water is disturbed at one focus of an elliptical water tank?
If the water's surface is disturbed at one focus of an elliptical water tank, the circular waves of that disturbance, after reflecting off the walls, converge simultaneously to a single point: the second focus. This is a consequence of the total travel length being the same along any wall-bouncing path between the two foci.
Who discovered that the planets orbit the Sun?
In the 17th century, Johannes Kepler discovered that the orbits along which the planets travel around the Sun are ellipses with the Sun [approximately] at one focus, in his first law of planetary motion. Later, Isaac Newton explained this as a corollary of his law of universal gravitation .
Overview
Parametric representation
Using trigonometric functions, a parametric representation of the standard ellipse is:
The parameter t (called the eccentric anomaly in astronomy) is not the angle of with the x-axis, but has a geometric meaning due to Philippe de La Hire (see Drawing ellipses below).
Definition as locus of points
An ellipse can be defined geometrically as a set or locus of points in the Euclidean plane:
Given two fixed points called the foci and a distance which is greater than the distance between the foci, the ellipse is the set of points such that the sum of the distances is equal to :
The midpoint of the line segment joining the foci is called the center of the ellipse. The line through the foci is called the major axis, and the line perpendicular to it through the center is the …
In Cartesian coordinates
The standard form of an ellipse in Cartesian coordinates assumes that the origin is the center of the ellipse, the x-axis is the major axis, and:
the foci are the points , the vertices are .
For an arbitrary point the distance to the focus is and to the other focus . Hence the point is on the ellipse whenever:
Eccentricity and the directrix property
Each of the two lines parallel to the minor axis, and at a distance of from it, is called a directrix of the ellipse (see diagram).
For an arbitrary point of the ellipse, the quotient of the distance to one focus and to the corresponding directrix (see diagram) is equal to the eccentricity:
The proof for the pair follows from the fact that and satisfy the equation
Focus-to-focus reflection property
An ellipse possesses the following property:
The normal at a point bisects the angle between the lines .
Proof
Because the tangent is perpendicular to the normal, the statement is true for the tangent and the supplementary angle of the angle between the lines to the foci (see diagram), too.
Conjugate diameters
A circle has the following property:
The midpoints of parallel chords lie on a diameter.
An affine transformation preserves parallelism and midpoints of line segments, so this property is true for any ellipse. (Note that the parallel chords and the diameter are no longer orthogonal.)
Definition
Orthogonal tangents
For the ellipse the intersection points of orthogonal tangents lie on the circle .
This circle is called orthoptic or director circle of the ellipse (not to be confused with the circular directrix defined above).