The word FOIL is an acronym for the four terms of the product:
- First (“first” terms of each binomial are multiplied together)
- Outer (“outside” terms are multiplied—that is, the first term of the first binomial and the second term of the second)
- Inner (“inside” terms are multiplied—second term of the first binomial and first term of the second)
- Last (“last” terms of each binomial are multiplied)
How do you foil math?
How to do Foil Method?
- F irst, which means multiplying the first terms together, i.e. ( a + b) ( c + d)
- O uter means that we multiply the outermost terms when the binomials are placed side by side, i.e. ( a + b) (c + d ).
- I nner means multiply the innermost terms together i.e. i.e. ...
- L ast. This implies that we multiply together the last term in each binomial, i.e., i.e. ...
What is an example of FOIL method?
- wisdom and foolishness
- calculating and impulsive
- stingy and generous
- thoughtful and inconsiderate
- adventurous and cautious
- aggressive and nonconfrontational
- ambitious and content
- shy and outgoing
- arrogant and humble
- law abider and law breaker
What does foil stand for in math?
In math, the acronym FOIL, meaning 'First, Outside, Inside, Last,' is a method used in multiplying two binomials. Learn about the FOIL method through the given examples and explanations. Updated: 12/22/2021 LOL! BFF! NFL! ABC! NASA! These are just a few popular acronyms that you may know.
How do you foil with 3 terms?
FOIL method. The FOIL Method is used to multiply binomials. F O I L is an acronym. The letters stand for First, Outside, Inside, and Last, referring to the order of multiplying terms. You multiply first terms, then outside terms, then inside terms, then last terms, and then combine like terms for your answer.
How do you do the FOIL method?
0:183:26The FOIL Method | Easiest way to Multiply Polynomials | AlgebraYouTubeStart of suggested clipEnd of suggested clipWe'll start simple multiply X plus 2 by 2 X plus 3 we start by multiplying the first two termsMoreWe'll start simple multiply X plus 2 by 2 X plus 3 we start by multiplying the first two terms together so x times 2x equals 2x squared. Next we multiply the outer terms x times 3 equals 3x.
What is the meaning of FOIL method in math?
First, Outside, Inside, LastIn math, the acronym FOIL, meaning 'First, Outside, Inside, Last,' is a method used in multiplying two binomials.
What is the FOIL method in Algebra 2?
First, Outside, Inside, LastWhen multiplying two binomials, you have to remember to multiply using the "FOIL" system (First, Outside, Inside, Last). This means you will need to multiply four different pairs of terms together to get your trinomial.
How do you know when to use the FOIL method?
8:3018:09Foil Method Algebra, Binomials, Trinomials, Polynomials ... - YouTubeYouTubeStart of suggested clipEnd of suggested clipNow let's say if you were to see an expression that looks like this 2x. Minus 3 raised to the thirdMoreNow let's say if you were to see an expression that looks like this 2x. Minus 3 raised to the third power. And you want to expand. And simplify how can you do it. There's two techniques that you can
How do you do FOIL math problems?
0:031:23FOIL Method for Multiplying Binomials - Distributive Property - YouTubeYouTubeStart of suggested clipEnd of suggested clipAnd what foil tells us to do is first multiply the first terms X and 3x x times 3x is 3x squaredMoreAnd what foil tells us to do is first multiply the first terms X and 3x x times 3x is 3x squared next we need to multiply the outer terms that is X and negative 7 x times negative 7 is negative 7x.
What is an example of a FOIL character?
A foil is a character in the story that contrasts with the protagonist. In Romeo and Juliet for instance, Mercutio is a foil to both Romeo and Tybalt, as he shares many of their traits but differs from them in key ways.
What grade do you learn FOIL?
FOIL is an acronym for “first,” “outer,” “inner” and “last,” all of which refer to the order in which students should multiply the numerals of each pair. This method can be used in fourth grade math to multiply two two-digit numbers, though the numbers in question must first be broken down into polynomials.
When you FOIL do you add or multiply?
MathHelp.com. That is, foil tells you to multiply the first terms in each of the parentheses, then multiply the two terms that are on the "outside" (furthest from each other), then the two terms that are on the "inside" (closest to each other), and then the last terms in each of the parentheses.
How do you FOIL to the power of 3?
2:185:48Cubing a Binomial - Taking a Binomial to the Third Power - YouTubeYouTubeStart of suggested clipEnd of suggested clipX minus 4 times X minus 4. So first thing you do is x times X and that gives you x squared. And thenMoreX minus 4 times X minus 4. So first thing you do is x times X and that gives you x squared. And then x times 4 or a negative 4 you could think of it. So that's negative 4x.
What does "foil" mean in math?
Many students and educators in the United States now use the word "FOIL" as a verb meaning "to expand the product ...
What is the foil method?
The FOIL method is a special case of a more general method for multiplying algebraic expressions using the distributive law. The word FOIL was originally intended solely as a mnemonic for high-school students learning algebra. The term appears in William Betz's 1929 text Algebra for Today, where he states:
What is the process of converting a product of two binomials into a sum of four monomia
The FOIL rule converts a product of two binomials into a sum of four (or fewer, if like terms are then combined) monomials. The reverse process is called factoring or factorization. In particular, if the proof above is read in reverse it illustrates the technique called factoring by grouping .
What is the meaning of "foil" in algebra?
In elementary algebra, FOIL is a mnemonic for the standard method of multiplying two binomials —hence the method may be referred to as the FOIL method. The word FOIL is an acronym for the four terms of the product: F irst ("first" terms of each binomial are multiplied together)
Can you foil a product with more than two summands?
The FOIL rule cannot be directly applied to expanding products with more than two multiplicands or multiplicands with more than two summands. However, applying the associative law and recursive foiling allows one to expand such products. For instance,
What is the Foil Method?
Many students will start thinking of a kitchen when they first hear a mention of the term foil.
How to do Foil Method?
The foil method is a technique used for remembering the steps required to multiply two binomials in an organized manner.
How do you distribute binomials using the foil method?
Let us put this method into perspective by multiplying two binomials, (a + b) and (c + d).
What is the acronym for multiplying polynomials?
We are still going to use the distributive property, but many students refer to the acronym, FOIL in order to remember the steps for multiplying binomials.
Does foil work with all polynomials?
This is not the only method used when multiplying polynomials and it doesn't work for all polynomials. It ONLY works with two binomials!
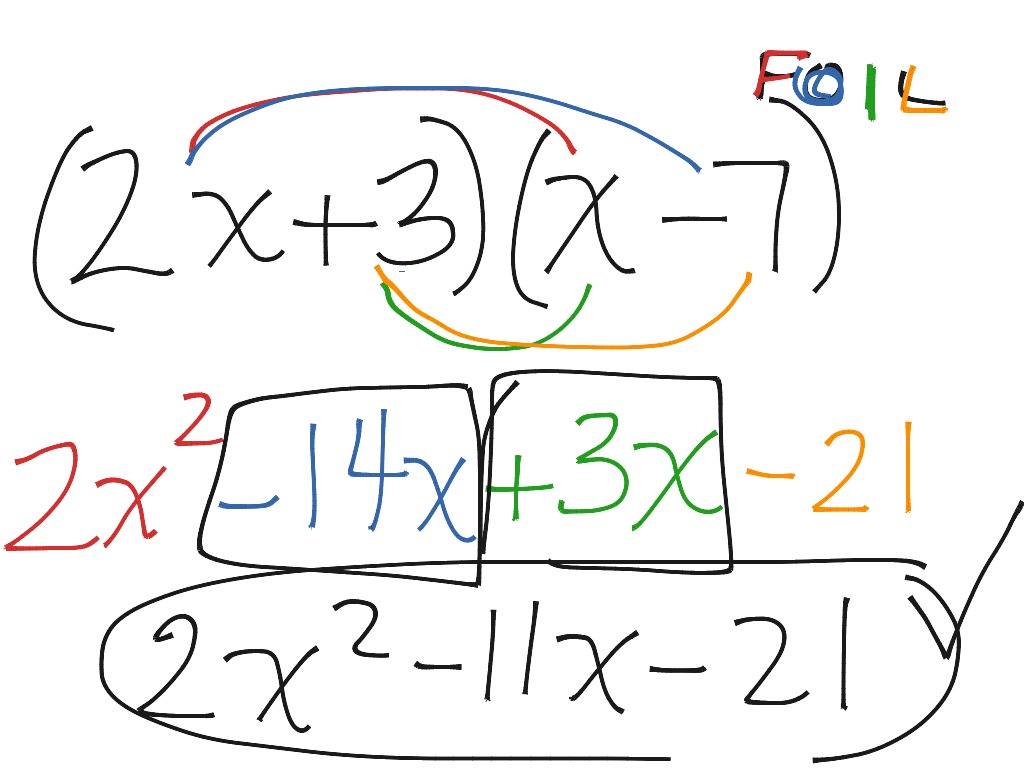
Overview
In secondary school, FOIL is a mnemonic for the standard method of multiplying two binomials —hence the method may be referred to as the FOIL method. The word FOIL is an acronym for the four terms of the product:
• First ("first" terms of each binomial are multiplied together)
• Outer ("outside" terms are multiplied—that is, the first term of the first binomial and the secon…
History
The FOIL method is a special case of a more general method for multiplying algebraic expressions using the distributive law. The word FOIL was originally intended solely as a mnemonic for high-school students learning algebra. The term appears in William Betz's 1929 text Algebra for Today, where he states:
... first terms, outer terms, inner terms, last terms. (The rule stated above may also be remember…
The FOIL method is a special case of a more general method for multiplying algebraic expressions using the distributive law. The word FOIL was originally intended solely as a mnemonic for high-school students learning algebra. The term appears in William Betz's 1929 text Algebra for Today, where he states:
... first terms, outer terms, inner terms, last terms. (The rule stated above may also be remember…
Examples
The method is most commonly used to multiply linear binomials. For example,
If either binomial involves subtraction, the corresponding terms must be negated. For example,
The distributive law
The FOIL method is equivalent to a two-step process involving the distributive law:
In the first step, the (c + d) is distributed over the addition in first binomial. In the second step, the distributive law is used to simplify each of the two terms. Note that this process involves a total of three applications of the distributive property. In contrast to the FOIL method, the method using distributive can be applied easily to products with more terms such as trinomials and higher.
Reverse FOIL
The FOIL rule converts a product of two binomials into a sum of four (or fewer, if like terms are then combined) monomials. The reverse process is called factoring or factorization. In particular, if the proof above is read in reverse it illustrates the technique called factoring by grouping.
Table as an alternative to FOIL
A visual memory tool can replace the FOIL mnemonic for a pair of polynomials with any number of terms. Make a table with the terms of the first polynomial on the left edge and the terms of the second on the top edge, then fill in the table with products. The table equivalent to the FOIL rule looks like this:
In the case that these are polynomials, (ax + b)(cx + d), the terms of a given degree are found by …
Generalizations
The FOIL rule cannot be directly applied to expanding products with more than two multiplicands or multiplicands with more than two summands. However, applying the associative law and recursive foiling allows one to expand such products. For instance,
Alternate methods based on distributing forgo the use of the FOIL rule, but may be easier to remember and apply. For example,
See also
• Binomial theorem
• Factorization