The cosine (sine complement, Latin: cosinus, sinus complementi) of an angle is the ratio of the length of the adjacent side to the length of the hypotenuse, so called because it is the sine of the complementary or co-angle, the other non-right angle.
Full Answer
When to use law of sines vs law of cosines?
Whenever you are given two angles, you can use the SINE LAW. Whenever you are given two sides, you can use the COSINE LAW. Some textbooks have a table of conditions to determine when to use which. I find that bordering on terror!
What is the difference between sine and cosine?
Sine is an odd function, and cosine is an even function. You may not have come across these adjectives “odd” and “even” when applied to functions, but it’s important to know them. A function f is said to be an odd function if for any number x, f (–x) = –f (x). What is maximum value of sin A? Maximum value of sin A is 1 when A = 90 degrees.
What are cosine rules?
New rules for isolation, testing and definitions for close contacts have come into effect this morning after leaders made a number of changes at an emergency national cabinet meeting on Thursday. After the meeting Prime Minister Scott Morrison said that ...
How to turn sine into cosine?
- (1) Memorize: sine = (opposite side) / hypotenuse.
- (2) sin A = cos (90° − A) or cos (π/2 − A) cos A = sin (90° − A) or sin (π/2 − A)
- (3) Memorize:
- (4) tangent = (opposite side) / (adjacent side)
- (5) Memorize:
- (6) tan A = cot (90° − A) or cot (π/2 − A)
- (7) sec A = csc (90° − A) or csc (π/2 − A)
What is the difference between sinus and cosinus?
Sine and cosine — a.k.a., sin(θ) and cos(θ) — are functions revealing the shape of a right triangle. Looking out from a vertex with angle θ, sin(θ) is the ratio of the opposite side to the hypotenuse , while cos(θ) is the ratio of the adjacent side to the hypotenuse .
How do you calculate sinus and cosinus?
Sin, Cos and TanThe sine of the angle = the length of the opposite side. the length of the hypotenuse.The cosine of the angle = the length of the adjacent side. the length of the hypotenuse.The tangent of the angle = the length of the opposite side. the length of the adjacent side.
What is sinus cosinus Tangens?
The cosine (often abbreviated "cos") is the ratio of the length of the side adjacent to the angle to the length of the hypotenuse. And the tangent (often abbreviated "tan") is the ratio of the length of the side opposite the angle to the length of the side adjacent.
What is cosine used for?
We can use the cosine rule to find the three unknown angles of a triangle if the three side lengths of the given triangle are known. We can also use the cosine rule to find the third side length of a triangle if two side lengths and the angle between them are known.
Why is it called sine?
The word sine originally came from the latin sinus, meaning "bay" or "inlet". However, it had a long path to get there. The earliest known reference to the sine function is from Aryabhata the Elder, who used both ardha-jya (half-chord) and jya (chord) to mean sine in Aryabhatiya, a Sanskrit text finished in 499 CE.
What is the value of tan A?
Deriving the Value of Tan DegreesAngles (in degrees)0°90°Sin01Cos10tan0Not Defined
What is csc sec and cot?
Csc sec cot are the three trigonometric functions cosecant, secant, and cotangent respectively. These functions are also called the reciprocal trigonometric functions as they are the reciprocals of the sine function, cosine function, and tangent function, respectively.
What is tan theta?
The law of Tangent which is also called as tangent formula or tangent rule is the ratio of the sine of the angle to the cos of the angle. Tan Θ = Opposite / Adjacent.
What is math Theta?
The Greek letter θ (theta) is used in math as a variable to represent a measured angle. For example, the symbol theta appears in the three main trigonometric functions: sine, cosine, and tangent as the input variable. cos(θ)
Where is the cosine rule used?
The sine rule is used when we are given either a) two angles and one side, or b) two sides and a non-included angle. The cosine rule is used when we are given either a) three sides or b) two sides and the included angle.
How do you explain the cosine rule?
3:2310:11The Cosine Rule - YouTubeYouTubeStart of suggested clipEnd of suggested clipThen we can substitute the numbers in so a squared is x squared equals 8 squared plus 12 squaredMoreThen we can substitute the numbers in so a squared is x squared equals 8 squared plus 12 squared minus 2 times 8 times 12 cos 33.
What is cos formula?
What is the cosine formula? The cosine formula to find the side of the triangle is given by: c = √[a2 + b2 – 2ab cos C] Where a,b and c are the sides of the triangle.
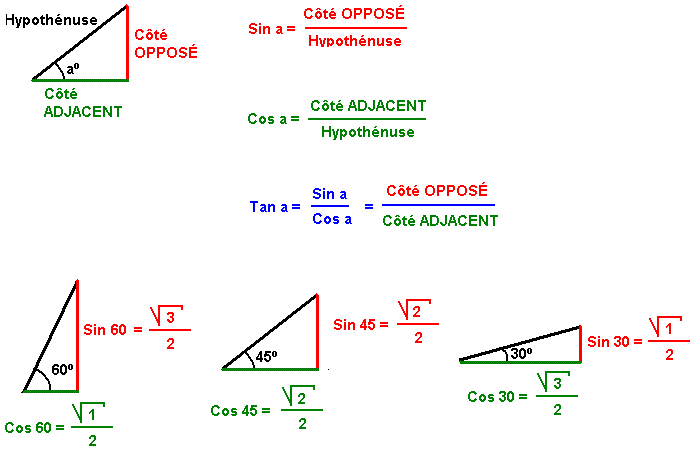
Right Triangle
Sine, Cosine and Tangent are the main functions used in Trigonometry and are based on a Right-Angled Triangle.
Sine, Cosine and Tangent
Sine, Cosine and Tangent (often shortened to sin, cos and tan) are each a ratio of sides of a right angled triangle:
Size Does Not Matter
The triangle can be large or small and the ratio of sides stays the same.
Angles From 0° to 360°
Move the mouse around to see how different angles (in radians or degrees) affect sine, cosine and tangent.
Examples
The classic 30° triangle has a hypotenuse of length 2, an opposite side of length 1 and an adjacent side of √ 3:
Exercise
Try this paper-based exercise where you can calculate the sine function for all angles from 0° to 360°, and then graph the result. It will help you to understand these relatively simple functions.
Less Common Functions
To complete the picture, there are 3 other functions where we divide one side by another, but they are not so commonly used.
Interactive Angles SOHCAHTOA
Try activating either ∠ A or ∠ B to explore the way that the adjacent and the opposite sides change based on the angle.
The Sine Ratio
Answer: sine of an angle is always the ratio of the o p p o s i t e s i d e h y p o t e n u s e .
The Cosine Ratio
The cosine of an angle is always the ratio of the (adjacent side/ hypotenuse).
The Tangent Ratio
The tangent of an angle is always the ratio of the (opposite side/ adjacent side).
Practice Problems
In the triangles below, identify the hypotenuse and the sides that are opposite and adjacent to the shaded angle.
Introduction
The solution for an oblique triangle can be done with the application of the Law of Sine and Law of Cosine, simply called the Sine and Cosine Rules. An oblique triangle, as we all know, is a triangle with no right angle. It is a triangle whose angles are all acute or a triangle with one obtuse angle.
Case 2: SSA or The Ambiguous Case
In this case, there may be two triangles, one triangle, or no triangle with the given properties. For this reason, it is sometimes called the ambiguous case. Thus, we need to examine the possibility of no solution, one or two solutions.
How do derivatives of trigonometric functions result from those of sine and cosine?
The derivatives of trigonometric functions result from those of sine and cosine by applying quotient rule. The values given for the antiderivatives in the following table can be verified by differentiating them. The number C is a constant of integration .
Where does the word "sine" come from?
The word sine derives from Latin sinus, meaning "bend; bay", and more specifically "the hanging fold of the upper part of a toga ", "the bosom of a garment", which was chosen as the translation of what was interpreted as the Arabic word jaib, meaning "pocket" or "fold" in the twelfth-century translations of works by Al-Battani and al-Khwārizmī into Medieval Latin. The choice was based on a misreading of the Arabic written form j-y-b ( جيب ), which itself originated as a transliteration from Sanskrit jīvā, which along with its synonym jyā (the standard Sanskrit term for the sine) translates to "bowstring", being in turn adopted from Ancient Greek χορδή "string".
What are the reciprocals of trigonometric functions?
Their reciprocals are respectively the cosecant, the secant, and the cotangent, which are less used. Each of these six trigonometric functions has a corresponding inverse function (called inverse trigonometric function ), and an equivalent in the hyperbolic functions as well.
What is trigonometric function?
In mathematics, the trigonometric functions (also called circular functions, angle functions or goniometric functions) are real functions which relate an angle of a right-angled triangle to ratios of two side lengths.
When were trigonometric functions first used?
While the early study of trigonometry can be traced to antiquity, the trigonometric functions as they are in use today were developed in the medieval period. The chord function was discovered by Hipparchus of Nicaea (180–125 BCE) and Ptolemy of Roman Egypt (90–165 CE). The functions of sine and versine (1 - cosine) can be traced back to the jyā and koti-jyā functions used in Gupta period Indian astronomy ( Aryabhatiya, Surya Siddhanta ), via translation from Sanskrit to Arabic and then from Arabic to Latin. (See Aryabhata's sine table .)
How to determine which formula to use
The goal of this page is to help students better understand when to use the Law of Sines and when to use the Law of Cosines
Practice Problems
Can you use the Law of Sines , the Law of Cosines , or neither to solve the unknown side in triangle 1 below?
Overview
In mathematics, sine and cosine are trigonometric functions of an angle. The sine and cosine of an acute angle are defined in the context of a right triangle: for the specified angle, its sine is the ratio of the length of the side that is opposite that angle to the length of the longest side of the triangle (the hypotenuse), and the cosine is the ratio of the length of the adjacent leg to that of the hypotenuse. Fo…
Notation
Sine and cosine are written using functional notation using the abbreviations sin and cos.
Definitions
To define the sine and cosine of an acute angle α, start with a right triangle that contains an angle of measure α; in the accompanying figure, angle α in triangle ABC is the angle of interest. The three sides of the triangle are named as follows:
• The opposite side is the side opposite to the angle of interest, in this case sid…
Identities
Exact identities (using radians):
These apply for all values of .
The reciprocal of sine is cosecant, i.e., the reciprocal of sin(A) is csc(A), or cosec(A). Cosecant gives the ratio of the length of the hypotenuse to the length of the opposite side. Similarly, the reciprocal of cosine is secant, which gives t…
Fixed points
Zero is the only real fixed point of the sine function; in other words the only intersection of the sine function and the identity function is . The only real fixed point of the cosine function is called the Dottie number. That is, the Dottie number is the unique real root of the equation The decimal expansion of the Dottie number is .
Law of sines
The law of sines states that for an arbitrary triangle with sides a, b, and c and angles opposite those sides A, B and C:
This is equivalent to the equality of the first three expressions below:
where R is the triangle's circumradius.
It can be proven by dividing the triangle into two right ones and using the above definition of sin…
Law of cosines
The law of cosines states that for an arbitrary triangle with sides a, b, and c and angles opposite those sides A, B and C:
In the case where , and this becomes the Pythagorean theorem: for a right triangle, where c is the hypotenuse.
Relationship to complex numbers
Sine and cosine are used to connect the real and imaginary parts of a complex number with its polar coordinates (r, φ):
The real and imaginary parts are:
where r and φ represent the magnitude and angle of the complex number z.
For any real number θ, Euler's formula says that:
Right Triangle
Sine, Cosine and Tangent
- Sine, Cosine and Tangent (often shortened to sin, cos and tan) are each a ratio of sidesof a right angled triangle: For a given angle θ each ratio stays the same no matter how big or small the triangle is To calculate them: Divide the length of one side by another side
Size Does Not Matter
- The triangle can be large or small and the ratio of sides stays the same. Only the angle changes the ratio. Try dragging point "A" to change the angle and point "B" to change the size: Good calculators have sin, cos and tan on them, to make it easy for you. Just put in the angle and press the button. But you still need to remember what they mean! In picture form:
Angles from 0° to 360°
- Move the mouse around to see how different angles (in radians or degrees) affect sine, cosine and tangent. In this animation the hypotenuse is 1, making the Unit Circle. Notice that the adjacent side and opposite side can be positive or negative, which makes the sine, cosine and tangent change between positive and negative values also.
Why?
- Why are these functions important? 1. Because they let us work out angles when we know sides 2. And they let us work out sides when we know angles
Exercise
- Try this paper-based exercisewhere you can calculate the sine function for all angles from 0° to 360°, and then graph the result. It will help you to understand these relatively simple functions. You can also see Graphs of Sine, Cosine and Tangent. And play with a spring that makes a sine wave.
Less Common Functions
- To complete the picture, there are 3 other functions where we divide one side by another, but they are not so commonly used. They are equal to 1 divided by cos, 1 divided by sin, and 1 divided by tan: