Is angular momentum proportional to the moment of inertia?
angular momentum L is proportional to moment of inertia I and angular speed ω measured in radians per second. Unlike mass, which depends only on amount of matter, moment of inertia is also dependent on the position of the axis of rotation and the shape of the matter.
Is angular momentum proportional to radius?
Angular momentum is directly proportional to square root of radius.Mar 17, 2019
Is angular momentum proportional to angular velocity?
Yes. Angular momentum L is directly proportional to angular velocity ω , with moment of inertia I being the constant of proportionality.Sep 14, 2015
Is angular momentum inversely proportional to mass?
With other variables held constant, as mass increases, angular momentum increases. Thus, mass is directly proportional to angular momentum.Aug 18, 2015
What happens to angular momentum if radius increases?
Yes, angular momentum of a rotating body changes with radius.Jul 27, 2018
How do you convert angular momentum to linear momentum?
Linear momentum (p) is defined as the mass (m) of an object multiplied by the velocity (v) of that object: p = m*v. With a bit of a simplification, angular momentum (L) is defined as the distance of the object from a rotation axis multiplied by the linear momentum: L = r*p or L = mvr.
How do you find change in angular momentum?
We can find the angular momentum by solvingnet τ=ΔLΔt net τ = Δ L Δ t for ΔL for ΔL, and using the given information to calculate the torque. The final angular momentum equals the change in angular momentum, because the lazy Susan starts from rest. That is, ΔL = L.
What is change in angular momentum?
Angular momentum is a vector that is parallel to the angular velocity. If there is no net torque acting on a system, the system's angular momentum is conserved. A net torque produces a change in angular momentum that is equal to the torque multiplied by the time interval over which the torque is applied.
What is the relation between linear momentum and angular momentum?
The main difference between linear momentum and angular momentum is that linear momentum is a property of an object which is in motion with respect to a reference point (i.e. any object changing its position with respect to the reference point) while angular momentum is a property of objects which are not only changing ...Nov 24, 2015
What does inversely proportional mean?
adjective. Britannica Dictionary definition of INVERSELY PROPORTIONAL. : related so that as one becomes larger the other becomes smaller.
What happens to angular momentum when mass doubles?
B) When mass is doubled, angular momentum doubles, so precession frequency decreases. B) If you increase radius, you increase angular momentum, and thus decrease the precession frequency.
What is the relationship between mass and momentum?
Mass and velocity are both directly proportional to the momentum. If you increase either mass or velocity, the momentum of the object increases proportionally. If you double the mass or velocity you double the momentum.
What is angular momentum?
Angular momentum, in physics, is a property that characterizes the rotatory inertia of an object in motion about the axis that may or may not pass through the specified object. The Earth’s rotation and revolution are the best real-life examples of angular momentum. For instance, the annual revolution that the Earth carries out about ...
Which rule gives the direction of angular momentum?
The right-hand thumb rule gives the direction of angular momentum and states that if someone positions his/her hand in a way that the fingers come in the direction of r, then the fingers on that hand curl towards the direction of rotation, and thumb points towards the direction of angular momentum (L), angular velocity, and torque.
What happens to velocity if no torque is applied?
Hence, if no torque is applied, then the perpendicular velocity of the object will alter according to the radius (the distance between the centre of the circle, and the centre of the mass of the body). It means velocity will be high for a shorter radius and low for a longer one. Share this with your friends. Share.
How is torque related to angular momentum?
Here, torque is defined as the rate of change of angular momentum. Torque is related to angular momentum in a way similar to how force is related to linear momentum. Now, when we know what the angular momentum and torque are, let's see how these two are related. To see this, we need to find out how objects in rotational motion get moving or spinning in the first position. Let's take the example of a wind turbine. We all know that it's the wind that makes the turbine spins. But how is it doing so? Well, the wind is pushing the turbine's blade by applying force to blades at some angles and radius from the axis of rotation of the turbine. In simple words, the wind is applying torque to the turbine. Hence, it is torque what gets rotatable objects spinning when they are standing still. Moreover, if the torque is applied to an object which is already spinning in the same direction in which it is spinning, it upsurges its angular velocity. Hence, we can say that torque is directly proportional to the angular velocity of a rotating body. Since torque can change the angular velocity, it can also change the amount of angular momentum as the angular momentum depends on the product of the moment of inertia and angular velocity. This is how torque is related to angular momentum.
What is the total angular momentum of a body?
The total angular momentum of a body is the sum of spin and orbital angular momentum. In another way, angular momentum is a vector quantity that requires both the magnitude and the direction. For an orbiting object, the magnitude of the angular momentum is equal to its linear momentum. It is given as the product of mass (m) and linear velocity (v) ...
What is the torque applied to a turbine?
In simple words, the wind is applying torque to the turbine. Hence, it is torque what gets rotatable objects spinning when they are standing still. Moreover, if the torque is applied to an object which is already spinning in the same direction in which it is spinning, it upsurges its angular velocity.
Is torque proportional to angular velocity?
Hence, we can say that torque is directly proportional to the angular velocity of a rotating body . Since torque can change the angular velocity, it can also change the amount of angular momentum as the angular momentum depends on the product of the moment of inertia and angular velocity.
What is the total angular momentum of a system of particles about the origin?
and each having momentum. then the total angular momentum of the system of particles about the origin is the vector sum of the individual angular momenta about the origin. That is,
What is the rate of change of the total angular momentum of a system?
Thus, (Figure) states that the rate of change of the total angular momentum of a system is equal to the net external torque acting on the system when both quantities are measured with respect to a given origin.
How many blades are in a propeller?
A propeller consists of two blades each 3.0 m in length and mass 120 kg each. The propeller can be approximated by a single rod rotating about its center of mass. The propeller starts from rest and rotates up to 1200 rpm in 30 seconds at a constant rate. (a) What is the angular momentum of the propeller at.
Is the angular momentum of a meteor constant?
Therefore, since. , the angular momentum is changing as a function of time. The torque on the meteor about the origin, however, is constant, because the lever arm. and the force on the meteor are constants.
What is angular momentum?
Angular momentum is a vector, pointing in the direction of the angular velocity. If there is no net torque acting on a system, the system's angular momentum is conserved. A net torque produces a change in angular momentum that is equal to the torque multiplied by the time interval during which the torque was applied. Impulse.
What is the initial angular momentum of a bicycle?
The initial angular momentum about a vertical axis is zero. If the person re-positions the bicycle wheel so its rotation axis is vertical, the wheel exerts a torque on the person during the re-positioning that makes the person spin in the opposite direction as the wheel.
What is the law of conservation of angular momentum?
The Law of Conservation of Angular Momentumstates that, when no external torques act on a system, the angular momentum of the system is conserved. Always remember that angular momentum is a vector when applying this law. Figure Skater. A spinning figure skater is an excellent example of angular momentum conservation.
What is the product of a torque and the time interval over which the torque acts?
Impulse. In a rotational situation, impulse is the product of a torque and the time interval over which the torque acts. Work (a torque acting over an angle) produces a change in kinetic energy. An impulse (a torque acting over a time interval) produces a change in angular momentum. τ= Iα.
What is the best way to observe momentum conservation?
Bicycle Wheel. A person standing on a turntable while holding a bicycle wheel is an excellent place to observe angular momentum conservation in action. The person is initially not rotating on the turntable, and the bicycle wheel is rotating about a horizontal axis.
Does Sarah have angular momentum?
Sarah's angular momentum before the collision equals the angular momentum of the system after the collision. It's not obvious that Sarah has an initial angular momentum, although she clearly has a linear momentum. That linear momentum can be transformed to an angular momentum the same way forces produce torques.
What is the difference between spin and orbital momentum?
Despite their important differences, there is a fundamental similarity between spin and orbital angular momentum: they are both the infinitesmal generators of the rotation operator. The difference is that now we have to consider simultaneous rotation acting on two very different spaces; the infinite-dimensional position state, and the finite-dimensional space of spin states. We have a physical sense that these two spaces should be distinct in some sense, unless there is some interaction that couples them; the motion of the particle moving freely through space shouldn't care whether it is internally spin-up or spin-down.
Is an electron a spin-1/2 particle?
An electron is a spin-1/2 particle , and it has two orthogonal spin states in addition to the spatial part of its wavefunction. We could represent its wavefunction as a two-component "column vector", but we use the word cautiously, since this is not a spatial vector; vectors in space must have three components.
What is the difference between angular momentum and mass?
Any object moving with mass possesses momentum. The only difference in angular momentum is that it deals with rotating or spinning objects.
What is an angular momentum quantum number?
It is a quantum number of an atomic orbital that decides the angular momentum and describes the size and shape of the orbital. The typical value ranges from 0 to 1.
Is angular momentum a vector quantity?
It is the property of a rotating body given by the product of the moment of inertia and the angular velocity of the rotating object. It is a vector quantity, which implies that here along with magnitude, the direction is also considered. Symbol. The angular momentum is a vector quantity, denoted by. Units.
Overview
Definition in classical mechanics
Just as for angular velocity, there are two special types of angular momentum of an object: the spin angular momentum is the angular momentum about the object's centre of mass, while the orbital angular momentum is the angular momentum about a chosen center of rotation. The Earth has an orbital angular momentum by nature of revolving around the Sun, and a spin angular moment…
Analogy to linear momentum
Angular momentum can be described as the rotational analog of linear momentum. Like linear momentum it involves elements of mass and displacement. Unlike linear momentum it also involves elements of position and shape.
Many problems in physics involve matter in motion about some certain point in space, be it in actual rotation about it, or simply moving past it, where it is desired to know what effect the mov…
Conservation of angular momentum
A rotational analog of Newton's third law of motion might be written, "In a closed system, no torque can be exerted on any matter without the exertion on some other matter of an equal and opposite torque." Hence, angular momentum can be exchanged between objects in a closed system, but total angular momentum before and after an exchange remains constant (is conserved).
Angular momentum in orbital mechanics
While in classical mechanics the language of angular momentum can be replaced by Newton's laws of motion, it is particularly useful for motion in central potential such as planetary motion in the solar system. Thus, the orbit of a planet in the solar system is defined by its energy, angular momentum and angles of the orbit major axis relative to a coordinate frame.
In astrodynamics and celestial mechanics, a massless (or per unit mass) angular momentum is …
Solid bodies
Angular momentum is also an extremely useful concept for describing rotating rigid bodies such as a gyroscope or a rocky planet. For a continuous mass distribution with density function ρ(r), a differential volume element dV with position vector r within the mass has a mass element dm = ρ(r)dV. Therefore, the infinitesimal angular momentum of this element is:
Angular momentum in general relativity
In modern (20th century) theoretical physics, angular momentum (not including any intrinsic angular momentum – see below) is described using a different formalism, instead of a classical pseudovector. In this formalism, angular momentum is the 2-form Noether charge associated with rotational invariance. As a result, angular momentum is not conserved for general curved spacetimes, …
Angular momentum in quantum mechanics
In quantum mechanics, angular momentum (like other quantities) is expressed as an operator, and its one-dimensional projections have quantized eigenvalues. Angular momentum is subject to the Heisenberg uncertainty principle, implying that at any time, only one projection (also called "component") can be measured with definite precision; the other two then remain uncertain. Because of this, th…
Angular Momentum
Angular Momentum Formula
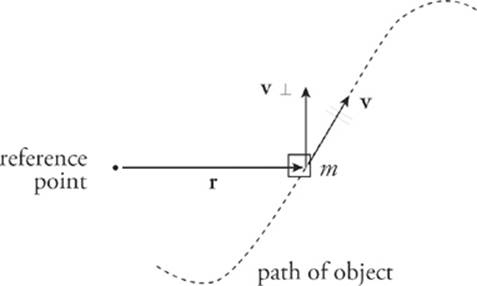
- The angular momentum of an object having mass (m) and linear velocity (v) with respect to a fixed point can be given as: L = mvr sin θ Or L→ = r x p→(in terms of vector product) Where, L→= Angular Momentum v = linear velocity of the object m = mass of the object p→= linear momentum r = radius, i.e., distance amid the object and the fixed point around which it revolves. Moreover, a…
Right-Hand Thumb Rule
- The right-hand thumb rule gives the direction of angular momentum and states that if someone positions his/her hand in a way that the fingers come in the direction of r, then the fingers on that hand curl towards the direction of rotation, and thumb points towards the direction of angular momentum (L), angular velocity, and torque.
Angular Momentum and Torque
- For a continuous rigid object, the total angular momentum is equal to the volume integral of angular momentum density over the entire object. Here, torque is defined as the rate of change of angular momentum. Torque is related to angular momentum in a way similar to how force is related to linear momentum. Now, when we know what the angular momentum and torque are, l…