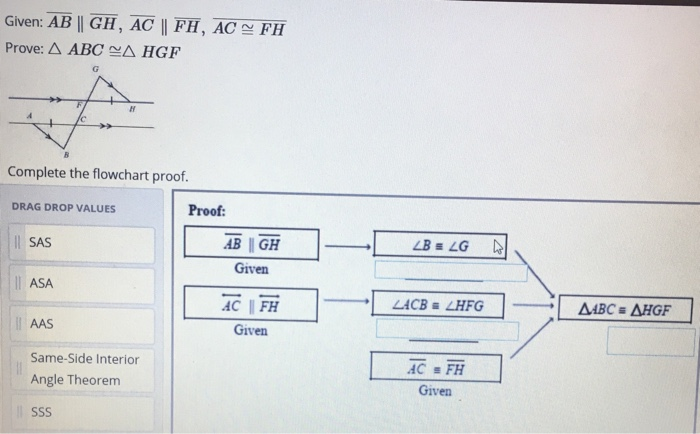
Flowchart proofs demonstrate geometry proofs by using boxes and arrows. In this method, statements are written inside boxes and reasons are written beneath each box. Unlike the other two proofs, flowcharts don't require you to write out every step and justification.
Full Answer
How to get good at proofs in geometry?
i. In a direct proof, the first thing you do is explicitly assume that the hypothesis is true for your selected variable, then use this assumption with definitions and previously proven results to show that the conclusion must be true. Direct Proof Walkthrough: Prove that if a is even, so is a2. Universally quantified implication: For all integers
What do you prove with a geometric proof?
- Make a game plan.
- Make up numbers for segments and angles.
- Look for congruent triangles (and keep CPCTC in mind).
- Try to find isosceles triangles.
- Look for parallel lines.
- Look for radii and draw more radii.
- Use all the givens.
- Check your if-then logic.
What is good way to approach proofs in geometry?
- Visual proof. Although not a formal proof, a visual demonstration of a mathematical theorem is sometimes called a " proof without words ".
- Elementary proof. ...
- Two-column proof. ...
- Statistical proof using data. ...
- Inductive logic proofs and Bayesian analysis. ...
- Proofs as mental objects. ...
- Influence of mathematical proof methods outside mathematics. ...
How do you write proofs for geometry?
Writing a proof consists of a few different steps. Draw the figure that illustrates what is to be proved. The figure may already be drawn for you, or you may have to draw it yourself. List the given statements, and then list the conclusion to be proved. Now you have a beginning and an end to the proof. Mark the figure according to what you can ...
What is a flow chart proof?
Lesson Summary. A flowchart proof is a formal proof that is set up with boxes that flow from one to the next with arrows. The statements, which are true facts that we know, are placed in the boxes, with the reason we know them on a line underneath.
How do you do flowchart proof?
1:2012:28Flowchart Thinking - YouTubeYouTubeStart of suggested clipEnd of suggested clipSo we have a pair of congruent angles that will help us in our proof. So now looking at the diagramMoreSo we have a pair of congruent angles that will help us in our proof. So now looking at the diagram we see that we have two pairs of congruent sides marked and a pair of congruent angles.
What does flowchart mean in geometry?
A flowchart is a formalized graphic representation of a logic sequence, work or manufacturing process, organization chart, or similar formalized structure.
What is a proof statement in geometry?
A two-column geometric proof consists of a list of statements, and the reasons that we know those statements are true. The statements are listed in a column on the left, and the reasons for which the statements can be made are listed in the right column.
What is the main parts of proof?
The most common form of explicit proof in highschool geometry is a two column proof consists of five parts: the given, the proposition, the statement column, the reason column, and the diagram (if one is given).
How do you fill out a flowchart in geometry?
2:3116:53Geometry 2.7a, Read & Write Flowchart proofs - YouTubeYouTubeStart of suggested clipEnd of suggested clipYou can mark it up you can figure out what the diagram is showing us and you can put in little tickMoreYou can mark it up you can figure out what the diagram is showing us and you can put in little tick marks for congruence. Or you know for segments or angles. So these are congruent segments.
What is a flowchart proof quizlet?
A flowchart proof. uses a visual representation of the logical flow of steps needed to reach a conclusion.
What is flowchart explain with example?
A flowchart is simply a graphical representation of steps. It shows steps in sequential order and is widely used in presenting the flow of algorithms, workflow or processes. Typically, a flowchart shows the steps as boxes of various kinds, and their order by connecting them with arrows.
What are paragraph proofs used for in geometry?
A paragraph proof is a way of presenting a mathematical proof. It consists of statements and reasons written as complete sentences in a paragraph. The reasons can be postulates, theorems, or other mathematical reasoning the reader is assumed to be able to follow without difficulty.
What are the 4 types of proofs in geometry?
Geometric ProofsGeometric Proofs.The Structure of a Proof.Direct Proof.Problems.Auxiliary Lines.Problems.Indirect Proof.Problems.
What are the 3 proofs in geometry?
Most geometry works around three types of proof:Paragraph proof.Flowchart proof.Two-column proof.
What is flow proof?
A flow proof is one of the ways that a proof can be formatted. The other two are a paragraph proof (in which the statements and reasons are written as sentences) and a two-column proof (in which the statements are written in one column and the reasons are written next to them in a second column). A flow proof, though, uses a diagram ...
What is proof in math?
Throughout the history of mathematics, a proof has been a series of statements that lead to a conclusion. Proofs begin with one or more given statements, which are provided. The given statement leads to other statements until the desired conclusion is reached. Each statement in a sequence must be supported with logical reasoning.
What is mathematical proof?
Mathematical proofs, or a series of statements that lead to a conclusion, use logical reasoning to support that a claim is true. When writing geometric proofs, it's important to have a good understanding of the definitions (like bisection, which is when one line cuts another line into two congruent parts), properties, and theorems used in geometry. ...
What is used to validate a statement in geometry?
Each statement in a sequence must be supported with logical reasoning. Mathematical properties, definitions, and theorems are used to validate the statements. When working with geometry proofs, it is important to be familiar with properties, definitions, and theorems that can be used to validate each statement.
Why are arrows drawn in a diagram?
Arrows are drawn to represent the sequence of the proof. The layout of the diagram is not important, but the arrows should clearly show how one statement leads to the next. The explanation for each statement is written below the statement. The following examples will detail each proof in paragraph form, followed by a flow chart.
Is EFH congruent to GFH?
This is enough information to prove that triangle EFH is congruent to triangle G FH according to the Side-Angle-Side theorem of congruent triangles. This means that each part of triangle EFH is congruent with its corresponding part in triangle GFH.
Why are flowchart proofs useful?
Flowchart proofs are useful because it allows the reader to see how each statement leads to the conclusion. There are 3 main ways to organize a proof in Geometry. The first way that isn't used that often is called the paragraph proof, the second way is called the two column proof and the third method is called flowchart proofs, ...
How are flowchart proofs organized?
Flowchart proofs are organized with boxes and arrows; each "statement" is inside the box and each " reason " is underneath each box. Each statement in a proof allows another subsequent statement to be made. In flowchart proofs, this progression is shown through arrows.
What is flowchart proof?
A flowchart proof is a series of boxes that are connected in a certain order to show the mathematical reasoning to prove something.
How to prove a flowchart?
To set up a flowchart proof, we start with any given information . Sometimes given information is found in a diagram and other times it is listed. The last box of the proof should contain the information we were trying to prove, with the reason we know that is true. We can prove theorems are true using flowchart proofs.
What are the vertical angle pairs?
The vertical angle pairs are angles 1 & 2 and angles 3 & 4. The Vertical Angles Theorem states that vertical angle pairs are congruent angles. Congruent angles are angles that have the same measure. Since this is a theorem, we can prove that it is true. We will use a flowchart proof to prove that vertical angles are always congruent.
What is flow proof?
A flow proof is just one representational style for the logical steps that go into proving a theorem or other proposition; rather than progress downward in two columns, as traditional proofs do, flow proofs utilize boxes and linking arrows to show the structure of the argument. All of the theorems, properties, definitions and postulates that support each step appear next to the boxes.
What is a two column proof?
The two-column proof is the traditional one used in high school geometry books, and it is also known as the ledger proof or the T-form proof. The shape, givens and task appear at the top of the page, but the columns "Statements" and "Reasons" take the reader through the proof step by step.
What is flowchart proof?
Also called the Flowchart Proof. This proof format shows the structure of a proof using boxes and connecting arrows. The appearance is like a detailed drawing of the proof. The justifications (the definitions, theorems, postulates and properties) are written beside the boxes.
What is geometric proof?
A geometric proof involves writing reasoned, logical explanations that use definitions, axioms, postulates, and previously proved theorems to arrive at a conclusion about a geometric statement.
How do flowchart proofs work?
Flowchart proofs demonstrate geometry proofs by using boxes and arrows. In this method, statements are written inside boxes and reasons are written beneath each box. Unlike the other two proofs, flowcharts don't require you to write out every step and justification.
What is geometric proof?
Geometry. , Mathematics. Geometric proofs are given statements that prove a mathematical concept is true. In order for a proof to be proven true, it has to include multiple steps. These steps are made up of reasons and statements. There are many types of geometric proofs, including two-column proofs, paragraph proofs, and flowchart proofs.
What are two column proofs?
Two-column, paragraph, and flowchart proofs are three of the most common geometric proofs. They each offer different ways of organizing reasons and statements so that each proof can be easily explained.
What is a paragraph proof?
Paragraph proofs are comprehensive paragraphs that explain the process of each proof. Like two-column proofs, they have multiple steps and justifications. But instead of columns, the given information is formatted like a word problem — written out in long-hand format.
Which theorem proves that triangles are congruent?
The columns above show how the shared midpoint, vertical angles of triangles FGH and IJH, and SAS (Side Angle Side) theorem prove the triangles are congruent.
What is geometric proof?
A geometric proof is a deduction reached using known facts such as axioms, postulates, lemmas, etc. with a series of logical statements. While proving any geometric proof statements are listed with the supporting reasons.
What is an equilateral triangle?
Solution. An equilateral triangle is a triangle in which all three sides are equal. Suppose that you have a segment XY X Y: You want to construct an equilateral triangle on XY X Y. Euclid’s third postulate says that a circle can be constructed with any center and any radius.