Full Answer
How did "normal" come to mean "perpendicular"?
When normal was first used it had nothing to do with people, or society, or human behavior. Norm and normal were Latin words used by mathematicians. Normal comes from the Latin word norma which refers to a carpenter’s square, or T-square. Building off the Latin, normal first meant “perpendicular” or “at right angles.”
What is the sign for perpendicular?
Perpendicular lines are lines, segments or rays that intersect to form right angles. The symbol ⊥ means is perpendicular to . The right angle symbol in the figure indicates that the lines are perpendicular. Does perpendicular mean opposite? Perpendicular lines have slopes that are the opposite of the reciprocal of each other.
What does it mean for a person to be dense?
- Estimated to detect about 1 additional cancer per 1,000 women
- Done at the same time as a standard mammogram
- Reduces the need for being called back for additional testing of areas of concern that aren't cancer
- Helpful in evaluating dense breast tissue
What is the symbol that means is perpendicular to?
- One of the angles in the diagram is a right angle.
- One of the orange-shaded angles is congruent to one of the green-shaded angles.
- Line c is perpendicular to line a.
- Line c is perpendicular to line b.
What is a perpendicular line?
What is Perpendicular? Two distinct lines intersecting each other at 90° or a right angle are called perpendicular lines. Example: Here, AB is perpendicular to XY because AB and XY intersect each other at 90°.
Where does the word "perpendicular" come from?
The word ‘perpendicular’ has its origin from the late Middle English which exactly means “at right angles”, from Latin ‘perpendicularis’, ‘perpendiculum’ meaning “plumb line” and from ‘perpendere’ where ‘per’ means “through” and ‘pendere’ means “to hang”. The perpendicular lines are always intersecting lines but intersecting lines are not always ...
Which side of a square is perpendicular to the other?
Adjacent sides of a square and a rectangle are always perpendicular to each other. Sides of the right-angled triangle enclosing the right angle are perpendicular to each other.
Do parallel lines intersect?
The two lines are parallel and do not intersect each other. They can never be perpendicular to each other. The two lines are intersecting each other at an acute angle. So, they are not perpendicular. The lines are not intersecting each other at right angles.
What is the definition of perpendicularity?
Perpendicularity is one particular instance of the more general mathematical concept of orthogonality; perpendicularity is the orthogonality of classical geometric objects.
How to tell if a line is perpendicular to another line?
A line is said to be perpendicular to another line if the two lines intersect at a right angle. Explicitly, a first line is perpendicular to a second line if (1) the two lines meet; and (2) at the point of intersection the straight angle on one side of the first line is cut by the second line into two congruent angles.
What is orthoptic property?
The orthoptic property of a parabola is that If two tangents to the parabola are perpendicular to each other, then they intersect on the directrix. Conversely, two tangents which intersect on the directrix are perpendicular. This implies that, seen from any point on its directrix, any parabola subtends a right angle.
How to find right angles in a two dimensional plane?
In the two-dimensional plane, right angles can be formed by two intersected lines if the product of their slopes equals −1. Thus defining two linear functions: y1 = a1x + b1 and y2 = a2x + b2, the graphs of the functions will be perpendicular and will make four right angles where the lines intersect if a1a2 = −1.
What is the perpendicularity of a right triangle?
The legs of a right triangle are perpendicular to each other. The altitudes of a triangle are perpendicular to their respective bases. The perpendicular bisectors of the sides also play a prominent role in triangle geometry. The Euler line of an isosceles triangle is perpendicular to the triangle's base.
What is the distance from a point to a line?
The distance from a point to a line is the distance to the nearest point on that line. That is the point at which a segment from it to the given point is perpendicular to the line.
Why are two lines parallel to each other?
Therefore, in Euclidean geometry, any two lines that are both perpendicular to a third line are parallel to each other, because of the parallel postulate . Conversely, if one line is perpendicular to a second line, it is also perpendicular to any line parallel to that second line.
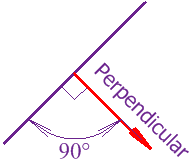
What Is perpendicular?
Perpendicular Symbol
- Perpendicular lines are represented by the symbol, ‘⊥’. Suppose, m andn are two lines intersecting each other at 90 degrees, then they are perpendicular to each other and are represented as m ⊥ n. The point of intersection of perpendicular lines is called the foot of the perpendicular.
Properties of Perpendicular Lines
- These lines always intersect at right angles.
- If two lines are perpendicular to the same line, they are parallel to each other and will never intersect.
Real-Life Examples
- We can observe many perpendicular lines in real life. Some examples are the sides of a set square, the arms of a clock, the corners of the blackboard, the window, and the Red Cross symbol.
Difference Between Perpendicular Lines and Parallel Lines
- Construction of Perpendicular Lines We can draw perpendicular lines for a given line in two ways. 1. Using a protractor 2. Using a compass Drawing a perpendicular line using a protractor Step 1: Let m be the given line and A the given point on it. Step 2: Place the protractor on the line m such that its baseline coincides with m, and its center falls on A. Step 3: Mark a point B against the 9…
Overview
In elementary geometry, two geometric objects are perpendicular if they intersect at a right angle (90 degrees or π/2 radians).
A line is said to be perpendicular to another line if the two lines intersect at a right angle. Explicitly, a first line is perpendicular to a second line if (1) the two lines meet; and (2) at the point of intersection the straight angle on one side of …
Foot of a perpendicular
The word foot is frequently used in connection with perpendiculars. This usage is exemplified in the top diagram, above, and its caption. The diagram can be in any orientation. The foot is not necessarily at the bottom.
More precisely, let A be a point and m a line. If B is the point of intersection of m and the unique line through A that is perpendicular to m, then B is called the foot of this perpendicular through A.
Construction of the perpendicular
To make the perpendicular to the line AB through the point P using compass-and-straightedge construction, proceed as follows (see figure left):
• Step 1 (red): construct a circle with center at P to create points A' and B' on the line AB, which are equidistant from P.
• Step 2 (green): construct circles centered at A' and B' having equal radius. Let Q and P be the points of intersection of the…
In relationship to parallel lines
If two lines (a and b) are both perpendicular to a third line (c), all of the angles formed along the third line are right angles. Therefore, in Euclidean geometry, any two lines that are both perpendicular to a third line are parallel to each other, because of the parallel postulate. Conversely, if one line is perpendicular to a second line, it is also perpendicular to any line parallel to that second line.
In computing distances
The distance from a point to a line is the distance to the nearest point on that line. That is the point at which a segment from it to the given point is perpendicular to the line.
Likewise, the distance from a point to a curve is measured by a line segment that is perpendicular to a tangent line to the curve at the nearest point on the curve.
Perpendicular regression fits a line to data points by minimizing the sum of squared perpendicul…
Graph of functions
In the two-dimensional plane, right angles can be formed by two intersected lines if the product of their slopes equals −1. Thus defining two linear functions: y1 = a1x + b1 and y2 = a2x + b2, the graphs of the functions will be perpendicular and will make four right angles where the lines intersect if a1a2 = −1. However, this method cannot be used if the slope is zero or undefined (the line is parallel to an axis).
In circles and other conics
Each diameter of a circle is perpendicular to the tangent line to that circle at the point where the diameter intersects the circle.
A line segment through a circle's center bisecting a chord is perpendicular to the chord.
If the intersection of any two perpendicular chords divides one chord into lengths a and b and divides the other chord into lengths c and d, then a + b + c + d equals the square of the diameter.
In polygons
The legs of a right triangle are perpendicular to each other.
The altitudes of a triangle are perpendicular to their respective bases. The perpendicular bisectors of the sides also play a prominent role in triangle geometry.
The Euler line of an isosceles triangle is perpendicular to the triangle's base.
The Droz-Farny line theorem concerns a property of two perpendicular lines intersecting at a trian…