Here are the rotation rules:
- 90° clockwise rotation: (x,y) becomes (y,-x)
- 90° counterclockwise rotation: (x,y) becomes (-y,x)
- 180° clockwise and counterclockwise rotation: (x, y) becomes (-x,-y)
- 270° clockwise rotation: (x,y) becomes (-y,x)
- 270° counterclockwise rotation: (x,y) becomes (y,-x)
- 90° clockwise rotation: (x,y) becomes (y,-x)
- 90° counterclockwise rotation: (x,y) becomes (-y,x)
- 180° clockwise and counterclockwise rotation: (x, y) becomes (-x,-y)
- 270° clockwise rotation: (x,y) becomes (-y,x)
- 270° counterclockwise rotation: (x,y) becomes (y,-x)
How to calculate rotation in geometry?
3 A (5, 2) B (- 2, 5) Now graph C, the image of A under a 180° counterclockwise rotation about the origin. Rule for 180° counterclockwise rotation:
What is the rule for 180 rotation?
Feb 18, 2022 · Here are the rotation rules: 90° clockwise rotation: (x,y) becomes (y,-x) 90° counterclockwise rotation: (x,y) becomes (-y,x) 180° clockwise and counterclockwise rotation: (x, y) becomes (-x,-y) 270° clockwise rotation: (x,y) becomes (-y,x) 270° counterclockwise rotation: (x,y) becomes (y,-x)
What are the rules for rotating shapes?
Jan 31, 2020 · There are some general rules for the rotation of objects using the most common degree measures (90 degrees, 180 degrees, and 270 degrees). The general rule for rotation of an object 90 degrees is (x, y) --------> (-y, x). Click to see full answer. Also …
What is the rotation rule for 270 degrees?
"Rotation" means turning around a center: The distance from the center to any point on the shape stays the same. Every point makes a circle around the center:
How to describe rotation?
To describe a rotation, you need three things: 1 Direction (clockwise CW or counterclockwise CCW) 2 Angle in degrees 3 Center point of rotation (turn about what point?)
What is the rotation of a figure?
A rotation is an isometric transformation that turns every point of a figure through a specified angle and direction about a fixed point. To describe a rotation, you need three things: Direction (clockwise CW or counterclockwise CCW) Angle in degrees.
What is the symmetry of a figure in a plane?
Rotational Symmetry. Lastly, a figure in a plane has rotational symmetry if the figure can be mapped onto itself by a rotation of 180° or less. This means that if we turn an object 180° or less, the new image will look the same as the original preimage.
What is rotation in math?
Rotation. The meaning of rotation in Maths is the circular motion of an object around a center or an axis. In real-life, we know the earth rotates on its own axis, which is also an example of rotation. In Geometry, there are four basic types of transformations. They are.
What direction does rotation take?
The rotation could be clockwise or counterclockwise . If there is an object which is to be rotated, it can be done by following different ways: 90 degrees clockwise. 90 degrees anticlockwise. 180 degrees clockwise. 180 degrees anticlockwise.
What is the meaning of rotation?
Rotation means the circular movement of an object around a center. It is possible to rotate different shapes by an angle around the center point. In three-dimensional shapes, the objects can be rotated about an infinite number of imaginary lines known as rotational axes.
What is the most common rotation angle?
Rotation can be done in both directions like clockwise as well as in counterclockwise. The most common rotation angles are 90°, 180° and 270°. There are certain rules for rotation in the coordinate plane. They are: Type of Rotation.
What is rotational symmetry?
All the regular polygons have rotational symmetry. If an object is rotated around its centre, the object appears exactly like before the rotation. Then the object is said to have rotational symmetry.
What is the purpose of a rotation matrix?
A rotation matrix is a matrix used to perform a rotation in a Euclidean space. In a two-dimensional cartesian coordinate plane system, the matrix R rotates the points in the XY-plane in the counterclockwise through an angle θ about the origin. The matrix R is given as,
Performing Geometry Rotations: Your Complete Guide
Welcome to this free lesson guide that accompanies this Geometry Rotations Explained Video Tutorial where you will learn the answers to the following key questions and information:
Rotation Geometry Definition
Rotation Geometry Definition: A rotation is a change in orientation based on the following possible rotations:
Geometry Clockwise Rotation Examples
Since the rotation is 90 degrees, you will rotating the point in a clockwise direction.
How to rotate a preimage?
2. In the above problem, the vertices of the pre-image are. 3. When we plot these points on a graph paper, we will get the figure of the pre-image (original figure). 4. When we rotate the given figure about 90° clock wise, we have to apply the formula. 5.
What are the three vertices of a triangle?
Let A ( -2, 1), B (2, 4) and C (4, 2) be the three vertices of a triangle. If this triangle is rotated about 90° clockwise, what will be the new vertices A' , B' and C' ?
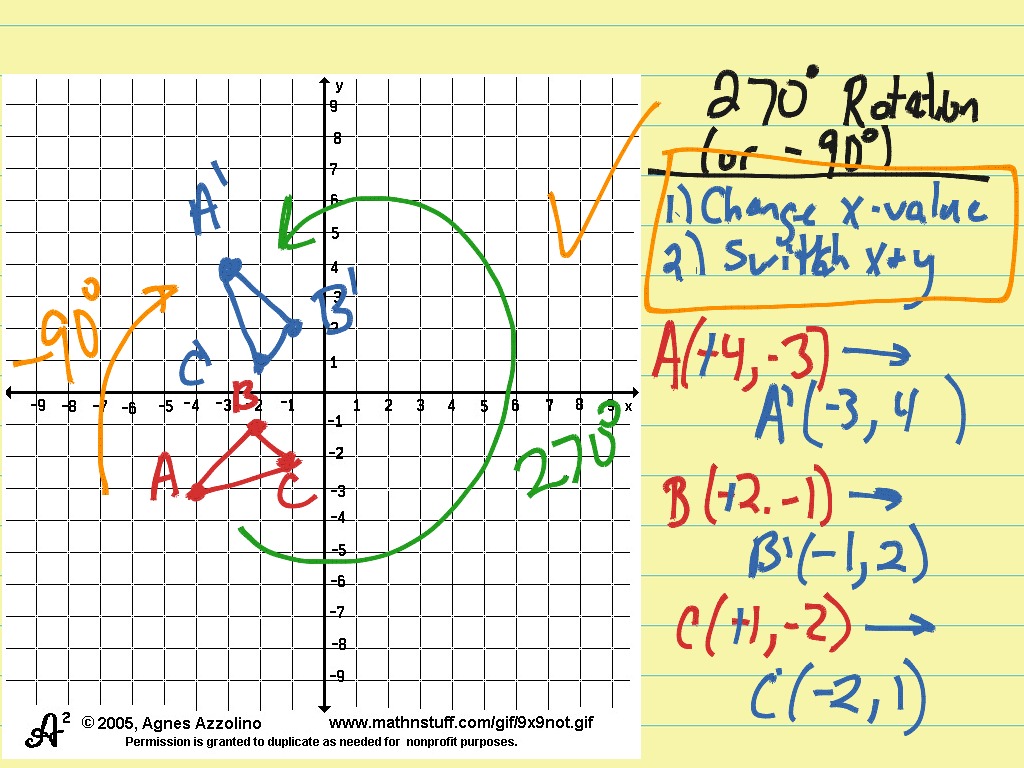
Rotations About The Origin
- 90 Degree Rotation
When rotating a point 90 degrees counterclockwise about the origin our point A(x,y) becomes A'(-y,x). In other words, switch x and y and make y negative. - 180 Degree Rotation
When rotating a point 180 degrees counterclockwise about the origin our point A(x,y) becomes A'(-x,-y). So all we do is make both x and y negative.
Composition of Transformations
- And just as we saw how two reflections back-to-back over parallel lines is equivalent to one translation, if a figure is reflected twice over intersecting lines, this composition of reflections is equal to one rotation. In fact, the angle of rotationis equal to twice that of the acute angle formed between the intersecting lines.
Rotational Symmetry
- Lastly, a figure in a plane has rotational symmetry if the figure can be mapped onto itself by a rotation of 180° or less. This means that if we turn an object 180° or less, the new image will look the same as the original preimage. And when describing rotational symmetry, it is always helpful to identify the order of rotations and the magnitude of rotations. The order of rotations is the nu…
Video – Lesson & Examples
- 38 min 1. Introduction to Rotations 2. 00:00:23– How to describe a rotational transformation (Examples #1-4) 3. Exclusive Content for Member’s Only 1. 00:12:12– Draw the image given the rotation (Examples #5-6) 2. 00:16:41– Find the coordinates of the vertices after the given transformation (Examples #7-8) 3. 00:19:03– How to describe the rotation after two repeated re…