how do you find a coterminal angle between 0 and 360

by Anastasia Osinski II Published 3 years ago Updated 3 years ago

To determine the coterminal angle between 0 and 360°, all you need to do is to use a modulo operation - in other words, divide your given angle by the 360° and check what the remainder is. We'll show you how it works with two examples - covering both positive and negative angles.

Coterminal angles are angles in standard positions (angles with the initial side on the positive x-axis) that have a common terminal side. For example, the angles 30°, -330°, and 390° are all coterminal. The coterminal angle for -86° between 0° and 360° is 360° - 86° = 274°.

Full Answer

How to find a positive and negative coterminal angle?

Do you want to find a coterminal angle of a given angle, preferably in the [0, 360°) range? ...
Are you hunting for positive and negative coterminal angles? ...
Would you like to check if two angles are coterminal? ...
Are you searching for a coterminal angles calculator for radians? ...
Or maybe you're looking for a coterminal angles definition, with some examples? ...

More items...

How to find the best angle?

The angles in a triangle (a 3-sided polygon) total 180 degrees.
The angles in a quadrilateral (a 4-sided polygon) total 360 degrees.
The angles in a pentagon (a 5-sided polygon) total 540 degrees.
The angles in a hexagon (a 6-sided polygon) total 720 degrees.
The angles in an octagon (an 8-sided polygon) total 1080 degrees.

How do you find the bisector of an angle?

Construct a circle centred at the intersection. Arbitrary size can do.
Construct two circles, respectively centred at the two intersections (of four) between circle and the two lines with the distance between them as the radius
Construct the bisector by joining the intersections (between two original lines, and between two circles constructed in 2)

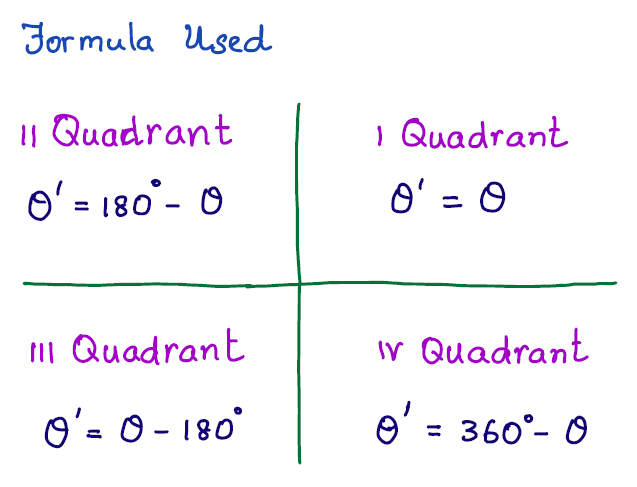
Which Angle has a positive measure?

As a first step, we determine its coterminal angle, which lies between 0° and 360°.
Next, we see the quadrant of the coterminal angle.
Whenever the terminal side is in the first quadrant (0° to 90°), the reference angle is the same as our given angle. ...

More items...

How do you find angles between 0 and 360 and is Coterminal with a angle?

1:532:50Example: Determine a Coterminal Angle Between 0 and 360 DegreesYouTubeStart of suggested clipEnd of suggested clipSo we could do is just take our angle 1524 degrees and then add multiples of 360 degrees times kMoreSo we could do is just take our angle 1524 degrees and then add multiples of 360 degrees times k where k is negative to obtain an angle that's between zero and 360 degrees.

How do you find the Coterminal angle?

In order to find a coterminal angle, or angles of the given angle, simply add or subtract 360 degrees of the terminal angle as many times as possible.

How do you find Coterminal angles with 360?

1:233:25How to determine two coterminal angles when above 360 degreesYouTubeStart of suggested clipEnd of suggested clipRight as many times as i want so there's infinite many coterminal angles infinite many so theMoreRight as many times as i want so there's infinite many coterminal angles infinite many so the directions. State find the smallest. Positive.

What is the measure of an angle between 0 360 degrees that is Coterminal with a 525 degree angle just type in numeric value?

For each given angle, find a coterminal angle with measure of θ such that 0° ≤ θ < 360°. Write 395° in terms of 360°. Write 525° in terms of 360°. So, the coterminal angle of 525° is 165°.

What is a Coterminal angle?

Coterminal angles: are angles in standard position (angles with the initial side on the positive x-axis) that have a common terminal side. For example, the angles 30°, –330° and 390° are all coterminal (see figure 2.1 below).

What is the Coterminal angle of 450?

Trigonometry Examples Subtract 360° 360 ° from 450° 450 ° . The resulting angle of 90° 90 ° is positive, less than 360° 360 ° , and coterminal with 450° 450 ° .

What is the Coterminal angle with 380 between 360 and 0?

Trigonometry Examples Subtract 360° 360 ° from 380° 380 ° . The resulting angle of 20° 20 ° is positive, less than 360° 360 ° , and coterminal with 380° 380 ° .

What is the measure of an angle between 0 and 360 that is Coterminal with 482?

The resulting angle of 122° 122 ° is positive, less than 360° 360 ° , and coterminal with 482° 482 ° .

What is the coordinate of 360?

1, 0Degrees = Θ(X,Y) coordinate300°(1/2, –√3/2)315°(-√2/2, –√2/2)330°(√3/2, –1/2)360°(1, 0)5 more rows

Which is the reference angle of θ =- 525 *?

Subtract 360° 360 ° from 525° 525 ° . The resulting angle of 165° 165 ° is positive, less than 360° 360 ° , and coterminal with 525° 525 ° .

Which angle is Coterminal with 112?

Some of the coterminal angles of 112° are 472°, 832°, -248°, and -608°.

How to find the coterminal angle of a given angle?

We determine the coterminal angle of a given angle by adding or subtracting 360° or 2π to it. In trigonometry, the coterminal angles have the same values for the functions of sin, cos, and tan.

What is a coterminal angle?

Coterminal angles are the angles that have the same initial side and share the terminal sides. The coterminal angles occupy the standard position, though their values are different. They are on the same sides, in the same quadrant and their vertices are identical.

Do coterminal angles have the same values?

In trigonometry, the coterminal angles have the same values for the functions of sin, cos, and tan. Once you have understood the concept, you will differentiate between coterminal angles and reference angles, as well as be able to solve problems with the coterminal angles formula. 1.

Is a coterminal angle positive or negative?

The coterminal angles can be positive or negative. In one of the above examples, we found that 390° and -690° are the coterminal angles of 30°. Here, 390° is the positive coterminal angle of 30° and. -690° is the negative coterminal angle of 30°.

What Are Coterminal Angles?

Angles that have the same initial side and share their terminal sides are coterminal angles. Although their values are different, the coterminal angles occupy the standard position. They are located in the same quadrant, have the same sides, and have the same vertices.

Conclusion

Angles that are coterminal can be positive and negative, as well as involve rotations of multiples of 360 degrees! Coterminal angles can be used to represent infinite angles in standard positions with the same terminal side.

FAQs

Coterminal Angles are angles that share the same initial side and terminal sides. Finding coterminal angles is as simple as adding or subtracting 360° or 2π to each angle, depending on whether the given angle is in degrees or radians.

Popular Posts:

1. qu es hablar literalmente ejemplos

2. antique grandfather clocks

3. did they cancel csi miami

4. t mobile phone plan cost

5. how to use re in a sentence

6. estudio profundo de la biblia

7. how much alcohol is in a mini fireball

8. 8 oz to 2 quarts

9. dove unscented baby soap

10. home depot thanksgiving decor

Params
0	`post`
1	`postContent`
2	`author`
3	`updated_at`
4	`bing_rich_snippet_text`
5	`bing_rich_snippet_link`
6	`bing_related_keywords`
7	`google_related_keywords`
8	`bing_news_title`
9	`bing_news_description`
10	`bing_videos`
11	`bing_images`
12	`bing_search_result_title`
13	`bing_search_result_description`
14	`bing_search_result_url`
15	`bing_paa_questions`
16	`bing_paa_answers`
17	`bing_slider_faq_questions`
18	`bing_slider_faq_answers`
19	`bing_pop_faq_questions`
20	`bing_pop_faq_answers`
21	`bing_tab_faq_questions`
22	`bing_tab_faq_answers`
23	`google_faq_questions`
24	`google_faq_answers`
25	`google_rich_snippet`
26	`google_search_result`
27	`indexedArray`
28	`total_images`
29	`total_videos`
30	`settings`
31	`url_current`
32	`menus`
33	`sidebar`

Params

post

postContent

author

updated_at

bing_rich_snippet_text

bing_rich_snippet_link

bing_related_keywords

google_related_keywords

bing_news_title

bing_news_description

bing_videos

bing_images

bing_search_result_title

bing_search_result_description

bing_search_result_url

bing_paa_questions

bing_paa_answers

bing_slider_faq_questions

bing_slider_faq_answers

bing_pop_faq_questions

bing_pop_faq_answers

bing_tab_faq_questions

bing_tab_faq_answers

google_faq_questions

google_faq_answers

google_rich_snippet

google_search_result

indexedArray

total_images

total_videos

settings

url_current

menus

sidebar

Params
0	`__env`
1	`app`
2	`errors`
3	`post`
4	`postContent`
5	`author`
6	`updated_at`
7	`bing_rich_snippet_text`
8	`bing_rich_snippet_link`
9	`bing_related_keywords`
10	`google_related_keywords`
11	`bing_news_title`
12	`bing_news_description`
13	`bing_videos`
14	`bing_images`
15	`bing_search_result_title`
16	`bing_search_result_description`
17	`bing_search_result_url`
18	`bing_paa_questions`
19	`bing_paa_answers`
20	`bing_slider_faq_questions`
21	`bing_slider_faq_answers`
22	`bing_pop_faq_questions`
23	`bing_pop_faq_answers`
24	`bing_tab_faq_questions`
25	`bing_tab_faq_answers`
26	`google_faq_questions`
27	`google_faq_answers`
28	`google_rich_snippet`
29	`google_search_result`
30	`indexedArray`
31	`total_images`
32	`total_videos`
33	`settings`
34	`url_current`
35	`menus`
36	`sidebar`
37	`i`
38	`__currentLoopData`
39	`loop`
40	`item`

Params

__env

app

errors

post

postContent

author

updated_at

bing_rich_snippet_text

bing_rich_snippet_link

bing_related_keywords

google_related_keywords

bing_news_title

bing_news_description

bing_videos

bing_images

bing_search_result_title

bing_search_result_description

bing_search_result_url

bing_paa_questions

bing_paa_answers

bing_slider_faq_questions

bing_slider_faq_answers

bing_pop_faq_questions

bing_pop_faq_answers

bing_tab_faq_questions

bing_tab_faq_answers

google_faq_questions

google_faq_answers

google_rich_snippet

google_search_result

indexedArray

total_images

total_videos

settings

url_current

menus

sidebar

__currentLoopData

loop

item

Params
0	`__env`
1	`app`
2	`errors`
3	`post`
4	`postContent`
5	`author`
6	`updated_at`
7	`bing_rich_snippet_text`
8	`bing_rich_snippet_link`
9	`bing_related_keywords`
10	`google_related_keywords`
11	`bing_news_title`
12	`bing_news_description`
13	`bing_videos`
14	`bing_images`
15	`bing_search_result_title`
16	`bing_search_result_description`
17	`bing_search_result_url`
18	`bing_paa_questions`
19	`bing_paa_answers`
20	`bing_slider_faq_questions`
21	`bing_slider_faq_answers`
22	`bing_pop_faq_questions`
23	`bing_pop_faq_answers`
24	`bing_tab_faq_questions`
25	`bing_tab_faq_answers`
26	`google_faq_questions`
27	`google_faq_answers`
28	`google_rich_snippet`
29	`google_search_result`
30	`indexedArray`
31	`total_images`
32	`total_videos`
33	`settings`
34	`url_current`
35	`menus`
36	`sidebar`
37	`i`
38	`__currentLoopData`
39	`loop`
40	`item`

Params

__env

app

errors

post

postContent

author

updated_at

bing_rich_snippet_text

bing_rich_snippet_link

bing_related_keywords

google_related_keywords

bing_news_title

bing_news_description

bing_videos

bing_images

bing_search_result_title

bing_search_result_description

bing_search_result_url

bing_paa_questions

bing_paa_answers

bing_slider_faq_questions

bing_slider_faq_answers

bing_pop_faq_questions

bing_pop_faq_answers

bing_tab_faq_questions

bing_tab_faq_answers

google_faq_questions

google_faq_answers

google_rich_snippet

google_search_result

indexedArray

total_images

total_videos

settings

url_current

menus

sidebar

__currentLoopData

loop

item

Params
0	`__env`
1	`app`
2	`errors`
3	`post`
4	`postContent`
5	`author`
6	`updated_at`
7	`bing_rich_snippet_text`
8	`bing_rich_snippet_link`
9	`bing_related_keywords`
10	`google_related_keywords`
11	`bing_news_title`
12	`bing_news_description`
13	`bing_videos`
14	`bing_images`
15	`bing_search_result_title`
16	`bing_search_result_description`
17	`bing_search_result_url`
18	`bing_paa_questions`
19	`bing_paa_answers`
20	`bing_slider_faq_questions`
21	`bing_slider_faq_answers`
22	`bing_pop_faq_questions`
23	`bing_pop_faq_answers`
24	`bing_tab_faq_questions`
25	`bing_tab_faq_answers`
26	`google_faq_questions`
27	`google_faq_answers`
28	`google_rich_snippet`
29	`google_search_result`
30	`indexedArray`
31	`total_images`
32	`total_videos`
33	`settings`
34	`url_current`
35	`menus`
36	`sidebar`
37	`i`
38	`__currentLoopData`
39	`loop`
40	`item`

Params

__env

app

errors

post

postContent

author

updated_at

bing_rich_snippet_text

bing_rich_snippet_link

bing_related_keywords

google_related_keywords

bing_news_title

bing_news_description

bing_videos

bing_images

bing_search_result_title

bing_search_result_description

bing_search_result_url

bing_paa_questions

bing_paa_answers

bing_slider_faq_questions

bing_slider_faq_answers

bing_pop_faq_questions

bing_pop_faq_answers

bing_tab_faq_questions

bing_tab_faq_answers

google_faq_questions

google_faq_answers

google_rich_snippet

google_search_result

indexedArray

total_images

total_videos

settings

url_current

menus

sidebar

__currentLoopData

loop

item

Params
0	`__env`
1	`app`
2	`errors`
3	`post`
4	`postContent`
5	`author`
6	`updated_at`
7	`bing_rich_snippet_text`
8	`bing_rich_snippet_link`
9	`bing_related_keywords`
10	`google_related_keywords`
11	`bing_news_title`
12	`bing_news_description`
13	`bing_videos`
14	`bing_images`
15	`bing_search_result_title`
16	`bing_search_result_description`
17	`bing_search_result_url`
18	`bing_paa_questions`
19	`bing_paa_answers`
20	`bing_slider_faq_questions`
21	`bing_slider_faq_answers`
22	`bing_pop_faq_questions`
23	`bing_pop_faq_answers`
24	`bing_tab_faq_questions`
25	`bing_tab_faq_answers`
26	`google_faq_questions`
27	`google_faq_answers`
28	`google_rich_snippet`
29	`google_search_result`
30	`indexedArray`
31	`total_images`
32	`total_videos`
33	`settings`
34	`url_current`
35	`menus`
36	`sidebar`
37	`i`
38	`__currentLoopData`
39	`loop`
40	`item`

Params

__env

app

errors

post

postContent

author

updated_at

bing_rich_snippet_text

bing_rich_snippet_link

bing_related_keywords

google_related_keywords

bing_news_title

bing_news_description

bing_videos

bing_images

bing_search_result_title

bing_search_result_description

bing_search_result_url

bing_paa_questions

bing_paa_answers

bing_slider_faq_questions

bing_slider_faq_answers

bing_pop_faq_questions

bing_pop_faq_answers

bing_tab_faq_questions

bing_tab_faq_answers

google_faq_questions

google_faq_answers

google_rich_snippet

google_search_result

indexedArray

total_images

total_videos

settings

url_current

menus

sidebar

__currentLoopData

loop

item

Params
0	`__env`
1	`app`
2	`errors`
3	`post`
4	`postContent`
5	`author`
6	`updated_at`
7	`bing_rich_snippet_text`
8	`bing_rich_snippet_link`
9	`bing_related_keywords`
10	`google_related_keywords`
11	`bing_news_title`
12	`bing_news_description`
13	`bing_videos`
14	`bing_images`
15	`bing_search_result_title`
16	`bing_search_result_description`
17	`bing_search_result_url`
18	`bing_paa_questions`
19	`bing_paa_answers`
20	`bing_slider_faq_questions`
21	`bing_slider_faq_answers`
22	`bing_pop_faq_questions`
23	`bing_pop_faq_answers`
24	`bing_tab_faq_questions`
25	`bing_tab_faq_answers`
26	`google_faq_questions`
27	`google_faq_answers`
28	`google_rich_snippet`
29	`google_search_result`
30	`indexedArray`
31	`total_images`
32	`total_videos`
33	`settings`
34	`url_current`
35	`menus`
36	`sidebar`
37	`i`
38	`__currentLoopData`
39	`loop`
40	`item`

Params

__env

app

errors

post

postContent

author

updated_at

bing_rich_snippet_text

bing_rich_snippet_link

bing_related_keywords

google_related_keywords

bing_news_title

bing_news_description

bing_videos

bing_images

bing_search_result_title

bing_search_result_description

bing_search_result_url

bing_paa_questions

bing_paa_answers

bing_slider_faq_questions

bing_slider_faq_answers

bing_pop_faq_questions

bing_pop_faq_answers

bing_tab_faq_questions

bing_tab_faq_answers

google_faq_questions

google_faq_answers

google_rich_snippet

google_search_result

indexedArray

total_images

total_videos

settings

url_current

menus

sidebar

__currentLoopData

loop

item

Params
0	`__env`
1	`app`
2	`errors`
3	`post`
4	`postContent`
5	`author`
6	`updated_at`
7	`bing_rich_snippet_text`
8	`bing_rich_snippet_link`
9	`bing_related_keywords`
10	`google_related_keywords`
11	`bing_news_title`
12	`bing_news_description`
13	`bing_videos`
14	`bing_images`
15	`bing_search_result_title`
16	`bing_search_result_description`
17	`bing_search_result_url`
18	`bing_paa_questions`
19	`bing_paa_answers`
20	`bing_slider_faq_questions`
21	`bing_slider_faq_answers`
22	`bing_pop_faq_questions`
23	`bing_pop_faq_answers`
24	`bing_tab_faq_questions`
25	`bing_tab_faq_answers`
26	`google_faq_questions`
27	`google_faq_answers`
28	`google_rich_snippet`
29	`google_search_result`
30	`indexedArray`
31	`total_images`
32	`total_videos`
33	`settings`
34	`url_current`
35	`menus`
36	`sidebar`
37	`i`
38	`__currentLoopData`
39	`loop`
40	`item`

Params

__env

app

errors

post

postContent

author

updated_at

bing_rich_snippet_text

bing_rich_snippet_link

bing_related_keywords

google_related_keywords

bing_news_title

bing_news_description

bing_videos

bing_images

bing_search_result_title

bing_search_result_description

bing_search_result_url

bing_paa_questions

bing_paa_answers

bing_slider_faq_questions

bing_slider_faq_answers

bing_pop_faq_questions

bing_pop_faq_answers

bing_tab_faq_questions

bing_tab_faq_answers

google_faq_questions

google_faq_answers

google_rich_snippet

google_search_result

indexedArray

total_images

total_videos

settings

url_current

menus

sidebar

__currentLoopData

loop

item

Metadata
Bindings	0. 2025-06-27 10:56:42 1. how-do-you-find-a-coterminal-angle-between-0-and-360
Backtrace	15. /app/Providers/RouteServiceProvider.php:54 18. /vendor/laravel/framework/src/Illuminate/Routing/Router.php:842 19. Route binding:39 20. /vendor/laravel/framework/src/Illuminate/Pipeline/Pipeline.php:167 21. /vendor/laravel/framework/src/Illuminate/Foundation/Http/Middleware/VerifyCsrfToken.php:78

Metadata

Bindings

0. 2025-06-27 10:56:42
1. how-do-you-find-a-coterminal-angle-between-0-and-360

Backtrace

15. /app/Providers/RouteServiceProvider.php:54
18. /vendor/laravel/framework/src/Illuminate/Routing/Router.php:842
19. Route binding:39
20. /vendor/laravel/framework/src/Illuminate/Pipeline/Pipeline.php:167
21. /vendor/laravel/framework/src/Illuminate/Foundation/Http/Middleware/VerifyCsrfToken.php:78

Metadata
Bindings	0. 193846 1. 0
Backtrace	19. middleware::checkdate:30 20. /vendor/laravel/framework/src/Illuminate/Pipeline/Pipeline.php:167 21. /vendor/laravel/jetstream/src/Http/Middleware/ShareInertiaData.php:61 22. /vendor/laravel/framework/src/Illuminate/Pipeline/Pipeline.php:167 23. /vendor/laravel/framework/src/Illuminate/Routing/Middleware/SubstituteBindings.php:50

Metadata

Bindings

0. 193846
1. 0

Backtrace

19. middleware::checkdate:30
20. /vendor/laravel/framework/src/Illuminate/Pipeline/Pipeline.php:167
21. /vendor/laravel/jetstream/src/Http/Middleware/ShareInertiaData.php:61
22. /vendor/laravel/framework/src/Illuminate/Pipeline/Pipeline.php:167
23. /vendor/laravel/framework/src/Illuminate/Routing/Middleware/SubstituteBindings.php:50

Metadata
Bindings	0. header
Backtrace	15. /vendor/outl1ne/nova-menu-builder/src/helpers.php:32 17. /vendor/laravel/framework/src/Illuminate/Routing/Controller.php:54 18. /vendor/laravel/framework/src/Illuminate/Routing/ControllerDispatcher.php:45 19. /vendor/laravel/framework/src/Illuminate/Routing/Route.php:261 20. /vendor/laravel/framework/src/Illuminate/Routing/Route.php:205

Metadata

Bindings

0. header

Backtrace

15. /vendor/outl1ne/nova-menu-builder/src/helpers.php:32
17. /vendor/laravel/framework/src/Illuminate/Routing/Controller.php:54
18. /vendor/laravel/framework/src/Illuminate/Routing/ControllerDispatcher.php:45
19. /vendor/laravel/framework/src/Illuminate/Routing/Route.php:261
20. /vendor/laravel/framework/src/Illuminate/Routing/Route.php:205

Metadata
Bindings	0. 1
Backtrace	19. /vendor/outl1ne/nova-menu-builder/src/Models/Menu.php:35 20. /vendor/outl1ne/nova-menu-builder/src/helpers.php:33 22. /vendor/laravel/framework/src/Illuminate/Routing/Controller.php:54 23. /vendor/laravel/framework/src/Illuminate/Routing/ControllerDispatcher.php:45 24. /vendor/laravel/framework/src/Illuminate/Routing/Route.php:261

Metadata

Bindings

0. 1

Backtrace

19. /vendor/outl1ne/nova-menu-builder/src/Models/Menu.php:35
20. /vendor/outl1ne/nova-menu-builder/src/helpers.php:33
22. /vendor/laravel/framework/src/Illuminate/Routing/Controller.php:54
23. /vendor/laravel/framework/src/Illuminate/Routing/ControllerDispatcher.php:45
24. /vendor/laravel/framework/src/Illuminate/Routing/Route.php:261

Metadata
Backtrace	24. /vendor/outl1ne/nova-menu-builder/src/Models/Menu.php:35 25. /vendor/outl1ne/nova-menu-builder/src/helpers.php:33 27. /vendor/laravel/framework/src/Illuminate/Routing/Controller.php:54 28. /vendor/laravel/framework/src/Illuminate/Routing/ControllerDispatcher.php:45 29. /vendor/laravel/framework/src/Illuminate/Routing/Route.php:261

Metadata

Backtrace

24. /vendor/outl1ne/nova-menu-builder/src/Models/Menu.php:35
25. /vendor/outl1ne/nova-menu-builder/src/helpers.php:33
27. /vendor/laravel/framework/src/Illuminate/Routing/Controller.php:54
28. /vendor/laravel/framework/src/Illuminate/Routing/ControllerDispatcher.php:45
29. /vendor/laravel/framework/src/Illuminate/Routing/Route.php:261

Metadata
Bindings	0. publish
Backtrace	14. /app/View/Composers/SidebarView.php:22 15. /app/View/Composers/SidebarView.php:12 16. /vendor/laravel/framework/src/Illuminate/View/Concerns/ManagesEvents.php:124 17. /vendor/laravel/framework/src/Illuminate/View/Concerns/ManagesEvents.php:162 20. /vendor/laravel/framework/src/Illuminate/View/Concerns/ManagesEvents.php:177

Metadata

Bindings

0. publish

Backtrace

14. /app/View/Composers/SidebarView.php:22
15. /app/View/Composers/SidebarView.php:12
16. /vendor/laravel/framework/src/Illuminate/View/Concerns/ManagesEvents.php:124
17. /vendor/laravel/framework/src/Illuminate/View/Concerns/ManagesEvents.php:162
20. /vendor/laravel/framework/src/Illuminate/View/Concerns/ManagesEvents.php:177

Metadata
Bindings	0. 19700
Backtrace	21. view::2dd102cf0462e89a4d4d8bc77355d767652bf9aa:15 23. /vendor/laravel/framework/src/Illuminate/Filesystem/Filesystem.php:108 24. /vendor/laravel/framework/src/Illuminate/View/Engines/PhpEngine.php:58 25. /vendor/livewire/livewire/src/ComponentConcerns/RendersLivewireComponents.php:69 26. /vendor/laravel/framework/src/Illuminate/View/Engines/CompilerEngine.php:61

Metadata

Bindings

0. 19700

Backtrace

21. view::2dd102cf0462e89a4d4d8bc77355d767652bf9aa:15
23. /vendor/laravel/framework/src/Illuminate/Filesystem/Filesystem.php:108
24. /vendor/laravel/framework/src/Illuminate/View/Engines/PhpEngine.php:58
25. /vendor/livewire/livewire/src/ComponentConcerns/RendersLivewireComponents.php:69
26. /vendor/laravel/framework/src/Illuminate/View/Engines/CompilerEngine.php:61

0 of 0

array:25 [▼"cookie" => array:1 [▶ 0 => "XSRF-TOKEN=eyJpdiI6Ik43OUVaaTlFYmpwWEtiK2NiRVlMeFE9PSIsInZhbHVlIjoickVPdjZlWVo0NU5vSkVSZm5hemtQMUgrSXo5cWF6Z1dNUWxXN3c3NEcyR0N0L1JML1czY2lqMGNXV3JGdWpTeTlYQTdqSWhDNTdlbHZPbUZwRHJncUc1Q0E4WjYrWStjZEZqMXBlZUVpRHpYUDlKVkdlTjFmMlZCV2d1WVk0VG0iLCJtYWMiOiI0YmQ2NGNkMWFhMDVkZmUzNjUyZTU4OWI3OTBiZmIzYmZlNTU2Y2NkODNmZTYyMzhlNWQxZDk2ODM4ODEwOTEwIiwidGFnIjoiIn0%3D; askhelpdesk_session=eyJpdiI6Im5wdzkwL1MzbnI1bjNoQ0Q1MjhobVE9PSIsInZhbHVlIjoiL1p1UlZ3cWtuejBLQUQ1UGd1Rm5HVFdxN1JiejJpOGJCQTRPR3Vvejh2a2hnRUswSDhRNDRudW1TUVVQdzZEbFVDSXNNdUZ5OUQ1TyszZEkrbW0xTS9id0NMY3dBNXY1b0hFQUErd3Rod1VNQ1E4TlBWZjJrL0FLc2pLck1QQkMiLCJtYWMiOiJjYWJkOTA0MDM1MTRlZGQyZTFmMWU5ODQ5YTJiZDkzY2RjMTI1ZmNhNWEwYWM3MDQ5M2Q2ZGVjYWIwYTliNzE2IiwidGFnIjoiIn0%3D; _pk_id.64.7c30=e380d979da1be2b5.1751002000.; _pk_ses.64.7c30=1 ◀XSRF-TOKEN=eyJpdiI6Ik43OUVaaTlFYmpwWEtiK2NiRVlMeFE9PSIsInZhbHVlIjoickVPdjZlWVo0NU5vSkVSZm5hemtQMUgrSXo5cWF6Z1dNUWxXN3c3NEcyR0N0L1JML1czY2lqMGNXV3JGdWpTeTlYQTdqS ▶" ] "cf-ipcountry" => array:1 [▶ 0 => "US" ] "cf-connecting-ip" => array:1 [▶ 0 => "216.73.216.235" ] "cdn-loop" => array:1 [▶ 0 => "cloudflare; loops=1" ] "sec-fetch-mode" => array:1 [▶ 0 => "navigate" ] "sec-fetch-site" => array:1 [▶ 0 => "none" ] "accept" => array:1 [▶ 0 => "text/html,application/xhtml+xml,application/xml;q=0.9,image/avif,image/webp,image/apng,*/*;q=0.8,application/signed-exchange;v=b3;q=0.7" ] "user-agent" => array:1 [▶ 0 => "Mozilla/5.0 AppleWebKit/537.36 (KHTML, like Gecko; compatible; ClaudeBot/1.0; +claudebot@anthropic.com)" ] "upgrade-insecure-requests" => array:1 [▶ 0 => "1" ] "sec-ch-ua-platform" => array:1 [▶ 0 => ""Windows"" ] "sec-ch-ua-mobile" => array:1 [▶ 0 => "?0" ] "sec-ch-ua" => array:1 [▶ 0 => ""Chromium";v="130", "HeadlessChrome";v="130", "Not?A_Brand";v="99"" ] "cache-control" => array:1 [▶ 0 => "no-cache" ] "pragma" => array:1 [▶ 0 => "no-cache" ] "accept-encoding" => array:1 [▶ 0 => "gzip, br" ] "cf-ray" => array:1 [▶ 0 => "956287f4fa0a9d52-ORD" ] "priority" => array:1 [▶ 0 => "u=0, i" ] "sec-fetch-dest" => array:1 [▶ 0 => "document" ] "sec-fetch-user" => array:1 [▶ 0 => "?1" ] "cf-visitor" => array:1 [▶ 0 => "{"scheme":"https"}" ] "connection" => array:1 [▶ 0 => "close" ] "x-forwarded-proto" => array:1 [▶ 0 => "https" ] "x-forwarded-for" => array:1 [▶ 0 => "216.73.216.235, 172.69.17.134" ] "x-server-addr" => array:1 [▶ 0 => "154.12.239.204" ] "host" => array:1 [▶ 0 => "receivinghelpdesk.com" ]]

0 of 0

array:56 [▼"USER" => "runcloud" "HOME" => "/home/runcloud" "SCRIPT_NAME" => "/ask/index.php" "REQUEST_URI" => "/ask/how-do-you-find-a-coterminal-angle-between-0-and-360" "QUERY_STRING" => "" "REQUEST_METHOD" => "GET" "SERVER_PROTOCOL" => "HTTP/1.0" "GATEWAY_INTERFACE" => "CGI/1.1" "REDIRECT_URL" => "/ask/how-do-you-find-a-coterminal-angle-between-0-and-360" "REMOTE_PORT" => "52552" "SCRIPT_FILENAME" => "/home/runcloud/webapps/ReceivingHelpDesk/ask/index.php" "SERVER_ADMIN" => "you@example.com" "CONTEXT_DOCUMENT_ROOT" => "/home/runcloud/webapps/ReceivingHelpDesk/" "CONTEXT_PREFIX" => "" "REQUEST_SCHEME" => "http" "DOCUMENT_ROOT" => "/home/runcloud/webapps/ReceivingHelpDesk/" "REMOTE_ADDR" => "172.69.17.134" "SERVER_PORT" => "80" "SERVER_ADDR" => "127.0.0.1" "SERVER_NAME" => "receivinghelpdesk.com" "SERVER_SOFTWARE" => "Apache/2.4.63 (Unix) OpenSSL/1.1.1f" "SERVER_SIGNATURE" => "" "LD_LIBRARY_PATH" => "/RunCloud/Packages/apache2-rc/lib" "PATH" => "/usr/local/sbin:/usr/local/bin:/usr/sbin:/usr/bin:/sbin:/bin" "HTTP_COOKIE" => "XSRF-TOKEN=eyJpdiI6Ik43OUVaaTlFYmpwWEtiK2NiRVlMeFE9PSIsInZhbHVlIjoickVPdjZlWVo0NU5vSkVSZm5hemtQMUgrSXo5cWF6Z1dNUWxXN3c3NEcyR0N0L1JML1czY2lqMGNXV3JGdWpTeTlYQTdqSWhDNTdlbHZPbUZwRHJncUc1Q0E4WjYrWStjZEZqMXBlZUVpRHpYUDlKVkdlTjFmMlZCV2d1WVk0VG0iLCJtYWMiOiI0YmQ2NGNkMWFhMDVkZmUzNjUyZTU4OWI3OTBiZmIzYmZlNTU2Y2NkODNmZTYyMzhlNWQxZDk2ODM4ODEwOTEwIiwidGFnIjoiIn0%3D; askhelpdesk_session=eyJpdiI6Im5wdzkwL1MzbnI1bjNoQ0Q1MjhobVE9PSIsInZhbHVlIjoiL1p1UlZ3cWtuejBLQUQ1UGd1Rm5HVFdxN1JiejJpOGJCQTRPR3Vvejh2a2hnRUswSDhRNDRudW1TUVVQdzZEbFVDSXNNdUZ5OUQ1TyszZEkrbW0xTS9id0NMY3dBNXY1b0hFQUErd3Rod1VNQ1E4TlBWZjJrL0FLc2pLck1QQkMiLCJtYWMiOiJjYWJkOTA0MDM1MTRlZGQyZTFmMWU5ODQ5YTJiZDkzY2RjMTI1ZmNhNWEwYWM3MDQ5M2Q2ZGVjYWIwYTliNzE2IiwidGFnIjoiIn0%3D; _pk_id.64.7c30=e380d979da1be2b5.1751002000.; _pk_ses.64.7c30=1 ◀XSRF-TOKEN=eyJpdiI6Ik43OUVaaTlFYmpwWEtiK2NiRVlMeFE9PSIsInZhbHVlIjoickVPdjZlWVo0NU5vSkVSZm5hemtQMUgrSXo5cWF6Z1dNUWxXN3c3NEcyR0N0L1JML1czY2lqMGNXV3JGdWpTeTlYQTdqS ▶" "HTTP_CF_IPCOUNTRY" => "US" "HTTP_CF_CONNECTING_IP" => "216.73.216.235" "HTTP_CDN_LOOP" => "cloudflare; loops=1" "HTTP_SEC_FETCH_MODE" => "navigate" "HTTP_SEC_FETCH_SITE" => "none" "HTTP_ACCEPT" => "text/html,application/xhtml+xml,application/xml;q=0.9,image/avif,image/webp,image/apng,*/*;q=0.8,application/signed-exchange;v=b3;q=0.7" "HTTP_USER_AGENT" => "Mozilla/5.0 AppleWebKit/537.36 (KHTML, like Gecko; compatible; ClaudeBot/1.0; +claudebot@anthropic.com)" "HTTP_UPGRADE_INSECURE_REQUESTS" => "1" "HTTP_SEC_CH_UA_PLATFORM" => ""Windows"" "HTTP_SEC_CH_UA_MOBILE" => "?0" "HTTP_SEC_CH_UA" => ""Chromium";v="130", "HeadlessChrome";v="130", "Not?A_Brand";v="99"" "HTTP_CACHE_CONTROL" => "no-cache" "HTTP_PRAGMA" => "no-cache" "HTTP_ACCEPT_ENCODING" => "gzip, br" "HTTP_CF_RAY" => "956287f4fa0a9d52-ORD" "HTTP_PRIORITY" => "u=0, i" "HTTP_SEC_FETCH_DEST" => "document" "HTTP_SEC_FETCH_USER" => "?1" "HTTP_CF_VISITOR" => "{"scheme":"https"}" "HTTP_CONNECTION" => "close" "HTTP_X_FORWARDED_PROTO" => "https" "HTTP_X_FORWARDED_FOR" => "216.73.216.235, 172.69.17.134" "HTTP_X_SERVER_ADDR" => "154.12.239.204" "HTTP_HOST" => "receivinghelpdesk.com" "HTTPS" => "on" "REDIRECT_STATUS" => "200" "REDIRECT_HTTPS" => "on" "FCGI_ROLE" => "RESPONDER" "PHP_SELF" => "/ask/index.php" "REQUEST_TIME_FLOAT" => 1751002002.7282 "REQUEST_TIME" => 1751002002]

0 of 0

array:4 [▼"XSRF-TOKEN" => "bHS4VqRkseoQjD9vN5LWrx304YSiqFAzl3v2xeas" "askhelpdesk_session" => "IsBXUyCjwiOippkxLOFE1thSn0OhMPUFihBXOlKL" "_pk_id_64_7c30" => null "_pk_ses_64_7c30" => null]

0 of 0

array:7 [▼"content-type" => array:1 [▶ 0 => "text/html; charset=UTF-8" ] "cache-control" => array:1 [▶ 0 => "private, must-revalidate" ] "date" => array:1 [▶ 0 => "Fri, 27 Jun 2025 05:26:42 GMT" ] "pragma" => array:1 [▶ 0 => "no-cache" ] "expires" => array:1 [▶ 0 => -1 ] "set-cookie" => array:2 [▶ 0 => "XSRF-TOKEN=eyJpdiI6IkxVNCtDTDJYcDMwcFpGcmdxM2ZPMlE9PSIsInZhbHVlIjoiNlMyM2RlNlNJNmtQVm5HVmlScG93Wk1mbXZpcGpSczZCSUI3SnZOVndEaVN3bi8rMmFOTjdpQXVuWlpxd3NYdDhIV1dBVnBCOTJWS0Y5S3VwVWVRS2hkVS8weHorQW5XZTd6R1NvQ285SnFyckRVSXdsZmFiUzEvQ3BYd2ZKRVIiLCJtYWMiOiI1NmQ4OTI3OGVlY2M0OTQyOTMxZWQwNDkzYTBkMzA5Y2I4N2Y0ODUzN2EzNmQ0NjMyMmE0ZGVjYzM4ZWY1ZGFiIiwidGFnIjoiIn0%3D; expires=Fri, 27-Jun-2025 07:26:43 GMT; Max-Age=7200; path=/; samesite=lax ◀XSRF-TOKEN=eyJpdiI6IkxVNCtDTDJYcDMwcFpGcmdxM2ZPMlE9PSIsInZhbHVlIjoiNlMyM2RlNlNJNmtQVm5HVmlScG93Wk1mbXZpcGpSczZCSUI3SnZOVndEaVN3bi8rMmFOTjdpQXVuWlpxd3NYdDhIV1dBV ▶" 1 => "askhelpdesk_session=eyJpdiI6InFmMzF0aEdPNVRaamJ6RmNMTTM3VVE9PSIsInZhbHVlIjoidGMvcjFzbHRNUUF6Tnk4TExqcytmYUhhTC94TFpXM1o3VzQxRkp4VUlINlpxa2x5a2VONTA2SVFucTdVUG5xemMyeUxQSmtKanpiQkVCL2k3aFF5ZURJY1ZTcjR1THllQkh6V1lhNnFQZkNSczJwYVRhRW00VUVaclhidjdmbVYiLCJtYWMiOiIxYjM0YjA1YWU3ZGU1ZDlkZmQ0OTAzYzZkMDU5M2NiM2ZkNTg1ZDI0MmE3ZGFiZDRmM2M1N2RlOTVjY2ExYzk1IiwidGFnIjoiIn0%3D; expires=Fri, 27-Jun-2025 07:26:43 GMT; Max-Age=7200; path=/; httponly; samesite=lax ◀askhelpdesk_session=eyJpdiI6InFmMzF0aEdPNVRaamJ6RmNMTTM3VVE9PSIsInZhbHVlIjoidGMvcjFzbHRNUUF6Tnk4TExqcytmYUhhTC94TFpXM1o3VzQxRkp4VUlINlpxa2x5a2VONTA2SVFucTdVUG5x ▶" ] "Set-Cookie" => array:2 [▶ 0 => "XSRF-TOKEN=eyJpdiI6IkxVNCtDTDJYcDMwcFpGcmdxM2ZPMlE9PSIsInZhbHVlIjoiNlMyM2RlNlNJNmtQVm5HVmlScG93Wk1mbXZpcGpSczZCSUI3SnZOVndEaVN3bi8rMmFOTjdpQXVuWlpxd3NYdDhIV1dBVnBCOTJWS0Y5S3VwVWVRS2hkVS8weHorQW5XZTd6R1NvQ285SnFyckRVSXdsZmFiUzEvQ3BYd2ZKRVIiLCJtYWMiOiI1NmQ4OTI3OGVlY2M0OTQyOTMxZWQwNDkzYTBkMzA5Y2I4N2Y0ODUzN2EzNmQ0NjMyMmE0ZGVjYzM4ZWY1ZGFiIiwidGFnIjoiIn0%3D; expires=Fri, 27-Jun-2025 07:26:43 GMT; path=/ ◀XSRF-TOKEN=eyJpdiI6IkxVNCtDTDJYcDMwcFpGcmdxM2ZPMlE9PSIsInZhbHVlIjoiNlMyM2RlNlNJNmtQVm5HVmlScG93Wk1mbXZpcGpSczZCSUI3SnZOVndEaVN3bi8rMmFOTjdpQXVuWlpxd3NYdDhIV1dBV ▶" 1 => "askhelpdesk_session=eyJpdiI6InFmMzF0aEdPNVRaamJ6RmNMTTM3VVE9PSIsInZhbHVlIjoidGMvcjFzbHRNUUF6Tnk4TExqcytmYUhhTC94TFpXM1o3VzQxRkp4VUlINlpxa2x5a2VONTA2SVFucTdVUG5xemMyeUxQSmtKanpiQkVCL2k3aFF5ZURJY1ZTcjR1THllQkh6V1lhNnFQZkNSczJwYVRhRW00VUVaclhidjdmbVYiLCJtYWMiOiIxYjM0YjA1YWU3ZGU1ZDlkZmQ0OTAzYzZkMDU5M2NiM2ZkNTg1ZDI0MmE3ZGFiZDRmM2M1N2RlOTVjY2ExYzk1IiwidGFnIjoiIn0%3D; expires=Fri, 27-Jun-2025 07:26:43 GMT; path=/; httponly ◀askhelpdesk_session=eyJpdiI6InFmMzF0aEdPNVRaamJ6RmNMTTM3VVE9PSIsInZhbHVlIjoidGMvcjFzbHRNUUF6Tnk4TExqcytmYUhhTC94TFpXM1o3VzQxRkp4VUlINlpxa2x5a2VONTA2SVFucTdVUG5x ▶" ]]

0 of 0

array:4 [▼"_token" => "bHS4VqRkseoQjD9vN5LWrx304YSiqFAzl3v2xeas" "_previous" => array:1 [▶ "url" => "https://receivinghelpdesk.com/ask/how-do-you-find-a-coterminal-angle-between-0-and-360" ] "_flash" => array:2 [▶ "old" => [] "new" => [] ] "PHPDEBUGBAR_STACK_DATA" => []]

1 x Application (97.92%)	972.56ms
1 x Booting (2.02%)	20.03ms