Graphing Rational Functions A. Test to see if the graph has symmetry by plugging in (-x) in the function. Options: If the signs all stay the same or all change, f(-x) = f(x), then you have even or y-axis symmetry. If either the numerator or the denominator changes signs completely, f(-x)= -f(x) then you have odd, or origin symmetry.
How to find the asymptotes of rational functions?
How to find the vertical asymptotes of a function?
- Factor the numerator and denominator.
- Observe any restrictions on the domain of the function.
- Simplify the expression by cancelling common factors in the numerator and denominator.
- Find any value that makes the denominator zero in the simplified version. This is where the vertical asymptotes occur.
How do you determine the symmetry of a function?
- Identify a and b for y = 1x2 + 2x. a = 1; b = 2
- Plug into the equation x = - b /2 a. x = -2/ (2*1)
- Simplify. x = -2/2
- The line of symmetry is x = -1.
What is the formula for rational function?
What Are Asymptotes?
- An asymptote is a line that the graph of the function approaches, but never touches.
- There are three types of asymptotes: horizontal, vertical, and oblique.
- Vertical asymptotes can be found out by finding the real zeros of the denominator.
- Horizontal asymptotes can be found out by thinking about the behavior of the function as x x approaches ±∞ ± ∞ .
How do you evaluate rational function?
Rational functions can be graphed on the coordinate plane. We can use algebraic methods to calculate their [latex]xlatex]-intercepts (also known as zeros or roots), which are points where the graph intersects the [latex]x[/latex]-axis. Rational functions can have zero, one, or multiple [latex]x[/latex]-intercepts.
Do rational graphs have symmetry?
2:388:15Learn how to graph a rational expression with symmetry about the ...YouTubeStart of suggested clipEnd of suggested clipAll you need to do is graph one side right and then you can just reflect it based on the symmetry.MoreAll you need to do is graph one side right and then you can just reflect it based on the symmetry. So to check for symmetry all we're simply going to do is evaluate for f of negative x.
Do all functions have symmetry?
1) Functions do not have to be symmetrical. So, they would not be even or odd. 2) If a function is even, it has symmetry around the y-axis.
How do you know if a function has symmetry?
How to Check For SymmetryFor symmetry with respect to the Y-Axis, check to see if the equation is the same when we replace x with −x:Use the same idea as for the Y-Axis, but try replacing y with −y.Check to see if the equation is the same when we replace both x with −x and y with −y.
What functions are symmetrical?
Functions can be symmetrical about the y-axis, which means that if we reflect their graph about the y-axis we will get the same graph. There are other functions that we can reflect about both the x- and y-axis and get the same graph. These are two types of symmetry we call even and odd functions.
Does an odd function have symmetry?
An odd function has rotational symmetry about the origin. We can decide algebraically if a function is even, odd or neither by replacing x by -x and computing f(-x). If f(-x) = f(x), the function is even.
Can a graph be symmetrical and not a function?
The other customary context for symmetry is judging from a graph whether a function is even or odd. Note: By definition, no function can be symmetric about the x-axis (or any other horizontal line), since anything that is mirrored around a horizontal line will violate the Vertical Line Test.
Which parent functions have symmetry?
In general, cubic functions will have a point of symmetry where the two other parts of the graph are mirror images of each other. The square root function is half of a side-opening parabola. The parent function has a vertex at (0, 0) and is only defined for x ≥ 0 in the real number system.
Can a function be odd and even?
Odd functions have graphs that are symmetric with respect to origin. Even functions have graphs that are symmetric with respect to y-axis. So, graph of f(x)=0 satisfies both conditions, therefore it is both odd and even.
What is an asymptote graph?
An asymptote is a line or curve which stupidly approaches the curve forever but yet never touches it. In fig. 1, an example of asymptotes is given.
What happens when Q (x) = 1?
When Q (x) = 1, i.e. a constant polynomial function, the rational function becomes a polynomial function.
What is rational quotient?
It is the quotient or ratio of two integers, where the denominator is not equal to zero. Hence, the name rational is derived from the word ratio.
What is horizontal asymptote?
Horizontal Asymptotes. This literally means that the asymptote is horizontal i.e. parallel to the axis of the independent variable. R (x) can only have a horizontal asymptote if. To determine the asymptotes, divide the numerator and the denominator of R (x) by .
Does R have an oblique asymptote?
R (x) will have oblique asymptote if it can be represented in the form .#N#When Q (x) ≫ 0, R (x) ≈ T (x). The curve or line T (x) hence becomes an oblique asymptote.
How to know if a rational function is zero?
A rational function will be zero at a particular value of x x only if the numerator is zero at that x x and the denominator isn’t zero at that x x. In other words, to determine if a rational function is ever zero all that we need to do is set the numerator equal to zero and solve.
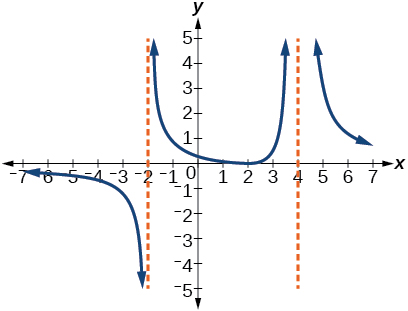
How to graph rational functions?
Process for Graphing a Rational Function 1 Find the intercepts, if there are any. Remember that the y y -intercept is given by (0,f (0)) ( 0, f ( 0)) and we find the x x -intercepts by setting the numerator equal to zero and solving. 2 Find the vertical asymptotes by setting the denominator equal to zero and solving. 3 Find the horizontal asymptote, if it exists, using the fact above. 4 The vertical asymptotes will divide the number line into regions. In each region graph at least one point in each region. This point will tell us whether the graph will be above or below the horizontal asymptote and if we need to we should get several points to determine the general shape of the graph. 5 Sketch the graph.
What is the vertical asymptote of a graph?
Here are the general definitions of the two asymptotes. The line x = a x = a is a vertical asymptote if the graph increases or decreases without bound on one or both sides of the line as x x moves in closer and closer to x = a x = a.
Why can odd functions not have a constant term?
Two things to keep in mind: 1) Odd functions cannot have a constant term because then the symmetry wouldn't be based on the origin. 2) Functions that are not polynomials or that don't have exponents can still be even or odd. For example, f (x)=cos (x) is an even function.
What is reflective symmetry?
A shape has reflective symmetry if it remains unchanged after a reflection across a line. For example, the pentagon above has reflective symmetry. Notice how line is a line of symmetry, and that the shape is a mirror image of itself across this line.
What is an even function?
Even functions. A function is said to be an even function if its graph is symmetric with respect to the -axis. For example, the function graphed below is an even function. Created with Raphaël Created with Raphaël. Created with Raphaël.
What does it mean when a function is odd?
Odd functions. A function is said to be an odd function if its graph is symmetric with respect to the origin. Visually, this means that you can rotate the figure about the origin, and it remains unchanged.
How to find asymptotes?
There are three types of asymptotes: horizontal, vertical, and oblique. Vertical asymptotes can be found out by finding the real zeros of the denominator. Horizontal asymptotes can be found out by thinking about the behavior of the function as x x approaches ±∞ ± ∞ . A rational function,
What is rational function?
A rational function is simply the ratio of polynomials. Any function of one variable, x, is called a rational function if, it can be represented as the following rational function formula: where p p and q q are polynomial functions of x x and q (x) ≠ 0 q (x) ≠ 0 .
Definitions
A function f ( x ) {\displaystyle f (x)} is called a rational function if and only if it can be written in the form
Taylor series
The coefficients of a Taylor series of any rational function satisfy a linear recurrence relation, which can be found by equating the rational function to a Taylor series with indeterminate coefficients, and collecting like terms after clearing the denominator.
Abstract algebra and geometric notion
In abstract algebra the concept of a polynomial is extended to include formal expressions in which the coefficients of the polynomial can be taken from any field. In this setting given a field F and some indeterminate X, a rational expression is any element of the field of fractions of the polynomial ring F [ X ].
Applications
Rational functions are used in numerical analysis for interpolation and approximation of functions, for example the Padé approximations introduced by Henri Padé. Approximations in terms of rational functions are well suited for computer algebra systems and other numerical software.